
7.诱导公式
可用十个字概括为“奇变偶不变,符号看象限”。
诱导公式一: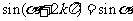 ,
,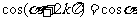 ,其中
,其中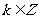

诱导公式二: 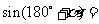
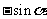 ;
; 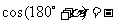
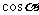
诱导公式三: 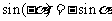 ;
; 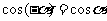
诱导公式四: ;
; 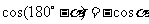

诱导公式五: ;
; 
|
|
-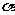 |
 |
 |
 |
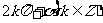 |
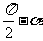 |
|
sin |
-sin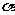 |
sin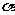 |
-sin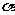 |
-sin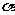 |
sin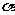 |
cos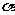 |
|
cos |
cos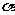 |
-cos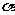 |
-cos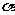 |
cos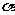 |
cos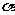 |
sin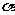 |
(1)要化的角的形式为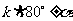 (
(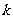 为常整数);
为常整数);
(2)记忆方法:“函数名不变,符号看象限”;
(3)sin(kπ+α)=(-1)ksinα;cos(kπ+α)=(-1)kcosα(k∈Z);
(4)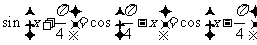 ;
;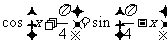 。
。
6.同角三角函数关系式
使用这组公式进行变形时,经常把“切”、“割”用“弦”表示,即化弦法,这是三角变换非常重要的方法。
几个常用关系式:sinα+cosα,sinα-cosα,sinα·cosα;(三式之间可以互相表示)
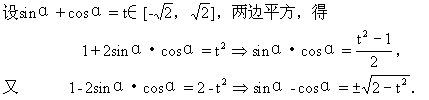
同理可以由sinα-cosα或sinα·cosα推出其余两式。
②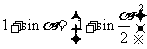 . ③当
. ③当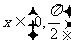 时,有
时,有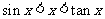 。
。
5.三角函数线
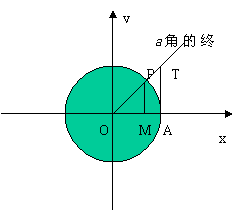 三角函数线是通过有向线段直观地表示出角的各种三角函数值的一种图示方法。利用三角函数线在解决比较三角函数值大小、解三角方程及三角不等式等问题时,十分方便。
三角函数线是通过有向线段直观地表示出角的各种三角函数值的一种图示方法。利用三角函数线在解决比较三角函数值大小、解三角方程及三角不等式等问题时,十分方便。
以坐标原点为圆心,以单位长度1为半径画一个圆,这个圆就叫做单位圆(注意:这个单位长度不一定就是1厘米或1米)。当角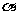 为第一象限角时,则其终边与单位圆必有一个交点
为第一象限角时,则其终边与单位圆必有一个交点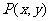 ,过点
,过点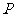 作
作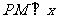 轴交
轴交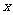 轴于点
轴于点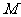 ,根据三角函数的定义:
,根据三角函数的定义: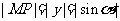 ;
;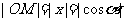 。
。
我们知道,指标坐标系内点的坐标与坐标轴的方向有关.当角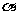 的终边不在坐标轴时,以
的终边不在坐标轴时,以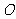 为始点、
为始点、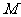 为终点,规定:
为终点,规定:
当线段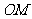 与
与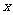 轴同向时,
轴同向时,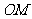 的方向为正向,且有正值
的方向为正向,且有正值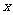 ;当线段
;当线段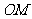 与
与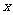 轴反向时,
轴反向时,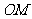 的方向为负向,且有正值
的方向为负向,且有正值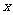 ;其中
;其中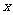 为
为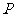 点的横坐标.这样,无论那种情况都有
点的横坐标.这样,无论那种情况都有
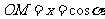
同理,当角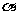 的终边不在
的终边不在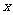 轴上时,以
轴上时,以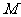 为始点、
为始点、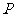 为终点,
为终点,
规定:当线段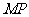 与
与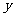 轴同向时,
轴同向时,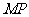 的方向为正向,且有正值
的方向为正向,且有正值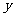 ;当线段
;当线段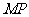 与
与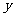 轴反向时,
轴反向时,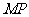 的方向为负向,且有正值
的方向为负向,且有正值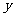 ;其中
;其中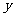 为
为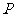 点的横坐标。
点的横坐标。
这样,无论那种情况都有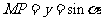 。像
。像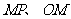 这种被看作带有方向的线段,叫做有向线段。
这种被看作带有方向的线段,叫做有向线段。
如上图,过点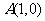 作单位圆的切线,这条切线必然平行于轴,设它与
作单位圆的切线,这条切线必然平行于轴,设它与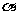 的终边交于点
的终边交于点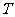 ,请根据正切函数的定义与相似三角形的知识,借助有向线段
,请根据正切函数的定义与相似三角形的知识,借助有向线段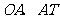 ,我们有
,我们有
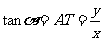
我们把这三条与单位圆有关的有向线段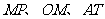 ,分别叫做角
,分别叫做角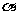 的正弦线、余弦线、正切线,统称为三角函数线。
的正弦线、余弦线、正切线,统称为三角函数线。
4.三角函数定义
在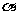 的终边上任取一点
的终边上任取一点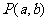 ,它与原点的距离
,它与原点的距离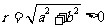 .过
.过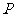 作
作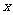 轴的垂线,垂足为
轴的垂线,垂足为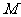 ,则线段
,则线段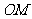 的长度为
的长度为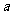 ,线段
,线段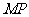 的长度为
的长度为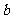 .则
.则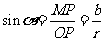 ;
;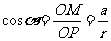 ;
;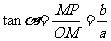 。
。
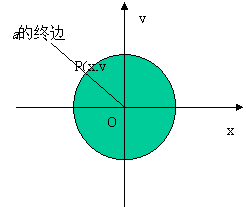 利用单位圆定义任意角的三角函数,设
利用单位圆定义任意角的三角函数,设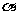 是一个任意角,它的终边与单位圆交于点
是一个任意角,它的终边与单位圆交于点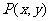 ,那么:
,那么:
(1)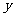 叫做
叫做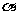 的正弦,记做
的正弦,记做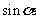 ,即
,即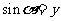 ;
;
(2)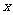 叫做
叫做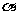 的余弦,记做
的余弦,记做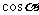 ,即
,即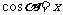 ;
;
(3)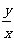 叫做
叫做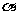 的正切,记做
的正切,记做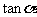 ,即
,即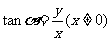 。
。
3.弧度制
长度等于半径长的圆弧所对的圆心角叫做1弧度角,记作1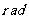 ,或1弧度,或1(单位可以省略不写)。
,或1弧度,或1(单位可以省略不写)。
角有正负零角之分,它的弧度数也应该有正负零之分,如-π,-2π等等,一般地, 正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0,角的正负主要由角的旋转方向来决定。
角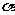 的弧度数的绝对值是:
的弧度数的绝对值是: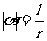 ,其中,l是圆心角所对的弧长,
,其中,l是圆心角所对的弧长,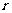 是半径。
是半径。
角度制与弧度制的换算主要抓住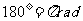 。
。
弧度与角度互换公式:1rad=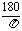 °≈57.30°=57°18ˊ、1°=
°≈57.30°=57°18ˊ、1°=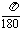 ≈0.01745(rad)。
≈0.01745(rad)。
弧长公式: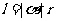 (
(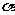 是圆心角的弧度数),
是圆心角的弧度数),
扇形面积公式: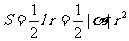 。
。
2.终边相同的角、区间角与象限角
角的顶点与原点重合,角的始边与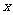 轴的非负半轴重合。那么,角的终边(除端点外)在第几象限,我们就说这个角是第几象限角。要特别注意:如果角的终边在坐标轴上,就认为这个角不属于任何一个象限,称为非象限角。
轴的非负半轴重合。那么,角的终边(除端点外)在第几象限,我们就说这个角是第几象限角。要特别注意:如果角的终边在坐标轴上,就认为这个角不属于任何一个象限,称为非象限角。
终边相同的角是指与某个角α具有同终边的所有角,它们彼此相差2kπ(k∈Z),即β∈{β|β=2kπ+α,k∈Z},根据三角函数的定义,终边相同的角的各种三角函数值都相等。
区间角是介于两个角之间的所有角,如α∈{α|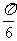 ≤α≤
≤α≤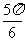 }=[
}=[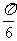 ,
,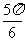 ]。
]。
1.任意角的概念
角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形。一条射线由原来的位置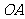 ,绕着它的端点
,绕着它的端点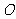 按逆时针方向旋转到终止位置
按逆时针方向旋转到终止位置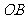 ,就形成角
,就形成角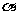 。旋转开始时的射线
。旋转开始时的射线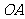 叫做角的始边,
叫做角的始边,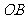 叫终边,射线的端点
叫终边,射线的端点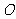 叫做叫
叫做叫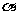 的顶点。
的顶点。
为了区别起见,我们规定:按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角。如果一条射线没有做任何旋转,我们称它形成了一个零角。
2.热点内容是三角函数知识的综合应用和实际应用,这也是新课标教材的热点内容。
从近几年的新课程高考考卷来看,试题内容主要考察三角函数的图形与性质,但解决这类问题的基础是任意角的三角函数及诱导公式,在处理一些复杂的三角问题时,同角的三角函数的基本关系式是解决问题的关键。
预测2007年高考对本讲的考察是:
1.题型是1道选择题和解答题中小过程;
2.三角函数
(1)借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义;
(2)借助单位圆中的三角函数线推导出诱导公式(π/2±α, π±α的正弦、余弦、正切)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com