
2.新课引入
哲学家卡尔.波普尔曾指出“科学与知识的增长永远始于问题,终于问题--愈来愈深化的问题,愈来愈能启发新问题的问题”,这对数学亦不例外。
因此,在新课的引入中首先提出问题“在直角坐标系内,平面内的每一个点都可以用一对实数(即它的坐标)来表示。同样,在平面直角坐标系内,每一个平面向量是否也可以用一对实数来表示?”,问题的给出旨在启发学生的思维。而学生思维是否到位,是否可以达到自己建构新知识的目的,取决于老师的引导是否得当。
1.提供新知识产生的理论基础
课堂教学论认为:要使教学过程最优化,首先要把已学的材料与学生已有的信息联系起来,使学生在学习新的材料时有适当的知识冗余。在本节之前,学生接触到的是向量的几何表示;向量共线的充要条件和平面向量的基本定理为引入向量的坐标运算奠定了理论基础。尤其是平面向量的基本定理,在新授课之前,我以为应再次跟学生进行强调,揭示其本质:即平面内的任一向量都可以表示为不共线的向量的线形组合。对于基底的理解,指出“基底不唯一,关键是不共线”。这样就使得新课的导入显得自然而不突兀,学生也很容易联想到基底选择的特殊性,从而引出坐标表示。
本节课尝试一种全新的教学模式,以建构主义理论为指导,教师在本节课中起的根本作用就是“为学生的学习创造一种良好的学习环境”,结合本节课是新授课的特点,我主要从以下几个方面做准备:(1)提供新知识产生的铺垫知识(2)模拟新知识产生过程中的细节和状态,启发引导学生主动建构(3)创设新知识思维发展的前景(4)通过“学习论坛时间”组织学生的合作学习、讨论学习、交流学习(5)通过“老师信箱时间”指导解答学生的疑难问题(6)通过“深化拓展区”培养学生的创新意识和发现能力。
整个过程学生始终处于交互式的学习环境中,让学生用自己的活动对已有的数学知识建构起自己的理解;让学生有了亲身参与的可能并且这种主动参与就为学生的主动性、积极性的发挥创造了很好的条件,真正实现了“学生是学习的主体”这一理念。
理解平面向量坐标化的意义是教学的难点;平面向量的坐标运算则是重点。我主要是采用启发引导式,并辅助适量的题组练习来帮助学生突破难点,强化重点。
2.能力方面:数形结合的思想和转化的思想
根据教学大纲的要求以及学生的实际知识水平,以期达到以下的目的:
1.知识方面:理解平面向量的坐标表示的意义;能熟练地运用坐标形式进行运算。
本节内容在教材中有着承上启下的作用,它是在学生对平面向量的基本定理有了充分的认识和正确的应用后产生的,同时也为下一节定比分点坐标公式和中点坐标公式的推导奠定了基础;向量用坐标表示后,对立体几何教材的改革也有着深远的意义,可使空间结构系统地代数化,把空间形式的研究从“定性”推到“定量”的深度。引入坐标运算之后使学生形成了完整的知识体系(向量的几何表示和向量的坐标表示),为用“数”的运算解决“形”的问题搭起了桥梁。
10. (2004.湖北理)已知6sin2α+sinαcosα-2cos2α=0,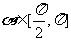 ,求
,求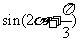 的值.
的值.
解法一:由已知得: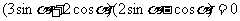
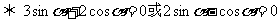
由已知条件可知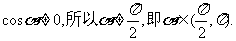
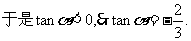



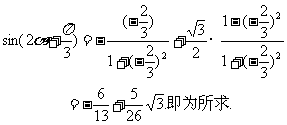
解法二:由已知条件可知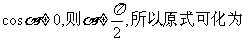

[探索题]求证: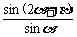 -2cos(α+β)=
-2cos(α+β)=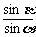 .
.
分析:先变形,只需证sin(2α+β)-2cos(α+β)·sinα=sinβ,再利用角的关系:2α+β=(α+β)+α,(α+β)-α=β可证得结论.
证明:sin(2α+β)-2cos(α+β)sinα
=sin[(α+β)+α]-2cos(α+β)sinα
=sin(α+β)cosα+cos(α+β)sinα-2cos(α+β)sinα
=sin(α+β)cosα-cos(α+β)sinα=sin[(α+β)-α]=sinβ.
两边同除以sinα得
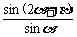 -2cos(α+β)=
-2cos(α+β)=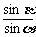 .
.
9. (2006年安徽)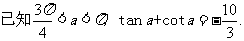
(Ⅰ)求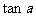 的值;
的值;
(Ⅱ)求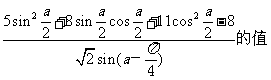 。
。
解:(Ⅰ)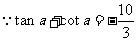 ,
,
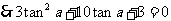 ,
,
解得
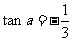 或
或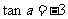 。
。
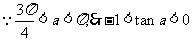
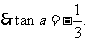
(II)
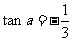 ,
,

=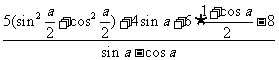
=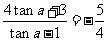
8.已知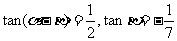 ,
,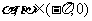 ,求2α-β.
,求2α-β.
解: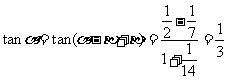 ,
,
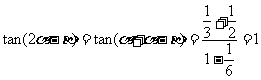
由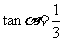 和
和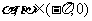 可知
可知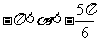 ,(这个范围必须足够精确)
,(这个范围必须足够精确)
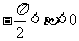 ,
,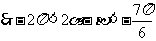
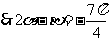
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com