
3、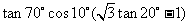 等于 ( )
等于 ( )
A、1 B、2 C、-1 D、-2
2、函数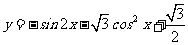 的最小正周期 ( )
的最小正周期 ( )
A、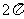 B、
B、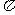 C、
C、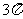 D、
D、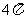
1、已知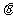 是第三象限角,且
是第三象限角,且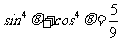 ,那么
,那么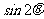 等于 ( )
等于 ( )
A、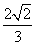 B、
B、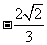 C、
C、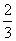 D、
D、
3、三角等式的证明:(1)三角恒等式的证题思路是根据等式两端的特征,通过三角恒等变换,应用化繁为简、左右同一等方法,使等式两端的化“异”为“同”;(2)三角条件等式的证题思路是通过观察,发现已知条件和待证等式间的关系,采用代入法、消参法或分析法进行证明。
2、三角函数的求值类型有三类:(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题;(2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如 等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。
等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。
1、三角函数式的化简:(1)常用方法:①直接应用公式进行降次、消项;②切割化弦,异名化同名,异角化同角;③ 三角公式的逆用等。(2)化简要求:①能求出值的应求出值;②使三角函数种数尽量少;③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数
本节课的教学重视发挥学生的主体作用与教师的主导作用,重视“过程”的教学,力求做到提出问题,循循善诱;疏通思路,耐心开导;解题练习,精心指导;存在不足,热情辅导;掌握过程,尽心引导。真正体现重情善导的教风与特色。
5.简单应用
在理解了向量坐标表示的实质意义后,通过学生的谈论和老师的指导,学生对本节的新知识有了系统的认识,都有跃跃欲试的心理,迫切希望在例题的应用中一显身手;另一方面,新的知识是在问题解决中不断发展的,而问题的解决又依赖于新知识作为理论基础,这种过程循环往复,既完善了新的知识又提高了学生的能力。所以,教师应抓住学生的心理,结合典型例题,充分展示新授知识所涉及到的各种题型。

 [ 例一 ] 如图,用基底
[ 例一 ] 如图,用基底 、
、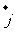 分别表示向量
分别表示向量 、
、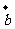 、
、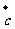 、
、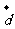 ,并求它们的坐标;
,并求它们的坐标;
方法一: =
=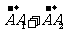 =2
=2 +3
+3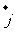 ,
,
 =(2,3)同理
=(2,3)同理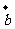 =(-2,3),
=(-2,3),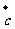 =(-2,-3),
=(-2,-3),
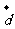 =(2,-3)
方法二:
=(2,-3)
方法二: A(2,2),B(4,5)
A(2,2),B(4,5)
 =(4,5)-(2,2)=(4-2,5-2)=
=(4,5)-(2,2)=(4-2,5-2)=
(2,3)
同理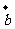 =(-2,3),
=(-2,3),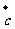 =(-2,-3),
=(-2,-3), =(2,-3)
方法三:
=(2,-3)
方法三:
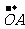 =(2,2),
=(2,2),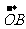 =(4,5)
=(4,5)
 =
=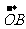 -
-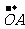 =(4,5)-(2,2)=(4-2,5-2)=(2,3)
同理
=(4,5)-(2,2)=(4-2,5-2)=(2,3)
同理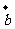 =(-2,3),
=(-2,3),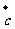 =(-2,-3),
=(-2,-3),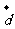 =(2,-3)(2,2)=(2,3)
问题(问题变换):(1)若点
=(2,-3)(2,2)=(2,3)
问题(问题变换):(1)若点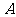 、
、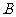 的坐标分别为
的坐标分别为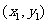 、
、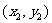 ,
,
那么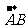 的坐标是
的坐标是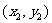 吗?(2)求出
吗?(2)求出 的坐标后,可以根据图形的什么特征,求出
的坐标后,可以根据图形的什么特征,求出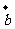 、
、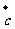 、
、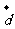 的坐标?
[ 说明 ] :还可根据对称性分别求出
的坐标?
[ 说明 ] :还可根据对称性分别求出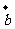 、
、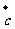 、
、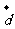 的坐标;
的坐标;

[ 例二 ] 已知 =(x+y+1,2x-y),
=(x+y+1,2x-y),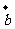 =(x-y,x+2y-2),若2
=(x-y,x+2y-2),若2 =3
=3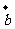 ,求x、y的值;
分析:本题检测向量相等的概念,利用条件2
,求x、y的值;
分析:本题检测向量相等的概念,利用条件2 =3
=3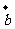 ,建立关于x、y的方程组,解方程组就可求x、y的值;
解:
,建立关于x、y的方程组,解方程组就可求x、y的值;
解: 2
2 =2(x+y+1,2x-y)=(2x+2y+2,4x-2y),3
=2(x+y+1,2x-y)=(2x+2y+2,4x-2y),3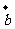 =3(x-y,x+2y-2)=(3x-3y,3x+6y-6),
=3(x-y,x+2y-2)=(3x-3y,3x+6y-6),
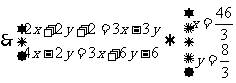
[ 例三 ] 已知平行四边形ABCD的三个顶点A、B、C的坐标分别为(-2,1)、(-1,3)、(3,4),求顶点D的坐标;
分析:本题检测如何用向量的终点和始点坐标求向量的坐标,并利用相等向量的坐标相同,建立等量关系求D点的坐标;
解:设D点坐标为(x,y)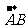 =(-1,3)-(-2,1)=(1,2)
=(-1,3)-(-2,1)=(1,2)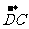 =(3,4)-(x,y)=(3-x,4-y)
由
=(3,4)-(x,y)=(3-x,4-y)
由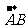 =
=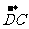 得1=3-x,2=4-y,所以x=2,y=2,即D点的坐标为(2,2)
6.深化拓展
得1=3-x,2=4-y,所以x=2,y=2,即D点的坐标为(2,2)
6.深化拓展
对于学有余力的同学,我提供了一个课外思考题。
已知:点A(2,3)、B(5,4)、C(7,10),若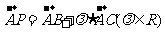 ,试求
,试求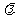 为何值时,点P在一、三象限角平分线上?点P在第三象限内?
为何值时,点P在一、三象限角平分线上?点P在第三象限内?
对于这个问题,我先不予提示,学生通过自己的思考和今天的新授知识会找到切实可行的方法,寻求问题的解答。
4.突破难点、突出重点
本节的学习中最难理解的就是向量与实数对之间的一一对应关系。为了突破该难点,我认为可以如此操作。通过动画设计,并结合向量相等的概念,指出任一向量总可以通过平移,使起点与原点重合。则向量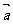 的坐标就是点A的坐标;反过来,点A的坐标也就是向量
的坐标就是点A的坐标;反过来,点A的坐标也就是向量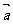 的坐标。揭示向量坐标表示的实质:相等的向量其坐标相同,坐标相同的向量是相等的向量。由此,向量与实数对之间的一一对应关系就不难理解了。
的坐标。揭示向量坐标表示的实质:相等的向量其坐标相同,坐标相同的向量是相等的向量。由此,向量与实数对之间的一一对应关系就不难理解了。

重点为向量的坐标运算。在理解了向量的坐标表示的实质后,学生很容易想到,向量的坐标运算其实也就是数量的代数运算。其运算法则,可以在“学习论坛时间”引导学生分组讨论自己推得。老师在学生推导的基础上进行指导和严格的归纳。如此一来,训练了学生独立思维、自主学习、交流互助的良好的学习习惯。
(1)两个向量和与差的坐标分别等于这两个向量相应坐标的和与差:
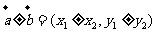 (其中
(其中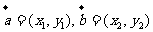 )
(2)一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标:
如果
)
(2)一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标:
如果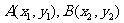 ,则
,则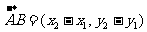 ;
(3)实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标:
若
;
(3)实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标:
若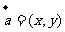 ,则
,则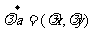 ;
;
3.创建新知识
以学生为主体绝不意味着老师可以袖手旁观,在创设问题情景后学生已进入激活状态,即想说但又不知道怎么说的状态,这时需老师适当加以点拨。指出:选择在平面直角坐标系内与坐标轴的正方向相同的两个单位向量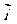 、
、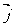 作为基底,任做一个向量
作为基底,任做一个向量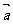 。由平面向量基本定理知,有并且只有一对实数x , y ,使
。由平面向量基本定理知,有并且只有一对实数x , y ,使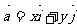
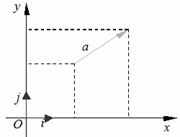 我们把 ( x , y ) 叫做向量
我们把 ( x , y ) 叫做向量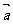 的(直角)坐标,记作
的(直角)坐标,记作 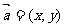
其中x叫做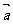 在 x 轴上的坐标,也叫做
在 x 轴上的坐标,也叫做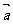 的第一分量;y叫
的第一分量;y叫
 做
做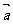 在y轴上的坐标,也叫做
在y轴上的坐标,也叫做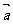 第二分量。
第二分量。
指导学生回答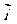 ,
, 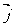 以及
以及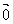 的坐标。
的坐标。
至此,完成向量的坐标表示的新知识的建构过程。整个过程决非把老师的认识强加给学生,而是把学生放在认知的主体地位,学生通过观察幻灯片的演示和老师的提示,思维得到了发展,观察、归纳能力得到了提高,对新授知识的理解更加清晰和深刻。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com