
1.对数函数的定义:
函数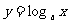
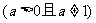 叫做对数函数;它是指数函数
叫做对数函数;它是指数函数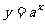
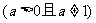 的反函数
的反函数
对数函数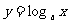
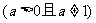 的定义域为
的定义域为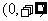 ,值域为
,值域为

3、我们研究指数函数时,曾经讨论过细胞分裂问题,某种细胞分裂时,得到的细胞的个数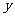 是分裂次数
是分裂次数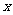 的函数,这个函数可以用指数函数
的函数,这个函数可以用指数函数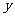 =
=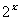 表示
表示
现在,我们来研究相反的问题,如果要求这种细胞经过多少次分裂,大约可以得到1万个,10万个……细胞,那么,分裂次数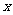 就是要得到的细胞个数
就是要得到的细胞个数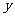 的函数
的函数 根据对数的定义,这个函数可以写成对数的形式就是
根据对数的定义,这个函数可以写成对数的形式就是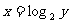
如果用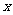 表示自变量,
表示自变量,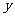 表示函数,这个函数就是
表示函数,这个函数就是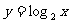
由反函数概念可知, 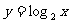 与指数函数
与指数函数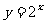 互为反函数
互为反函数
这一节,我们来研究指数函数的反函数对数函数
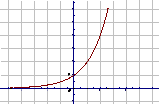
2、 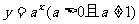 的图象和性质
的图象和性质
|
|
a>1 |
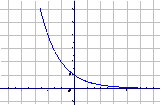
0<a<1 |
|
图 象 |
 |
 |
|
性 质 |
(1)定义域:R |
|
|
(2)值域:(0,+∞) |
||
|
(3)过点(0,1),即x=0时,y=1 |
||
|
(4)在 R上是增函数 |
(4)在R上是减函数 |
1、指对数互化关系:

课本第21页 习题1.5 1. 3. 5
思考题:解关于x的不等式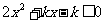
分析 此不等式为含参数k的不等式,当k值不同时相应的二次方程的判别式的值也不同,故应先从讨论判别式入手.
解 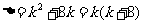
(1) 当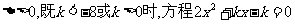 有两个不相等的实根.
有两个不相等的实根.
所以不等式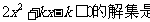 :
:
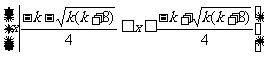
(2) 当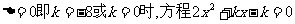 有两个相等的实根,
有两个相等的实根,
所以不等式 ,即
,即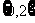 ;
;
(3) 当 无实根
无实根
所以不等式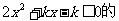 解集为
解集为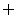 .
.
说明 一元二次方程、一元二次不等式、一元二次函数有着密切的联系,要注意数形结合研究问题.
解一元二次不等式的步骤:
① 将二次项系数化为“+”:A=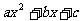 >0(或<0)(a>0)
>0(或<0)(a>0)
② 计算判别式 ,分析不等式的解的情况:
,分析不等式的解的情况:
ⅰ. >0时,求根
>0时,求根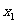 <
<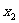 ,
,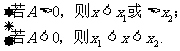
ⅱ. =0时,求根
=0时,求根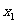 =
=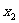 =
=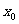 ,
,
ⅲ. <0时,方程无解,
<0时,方程无解,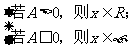
③ 写出解集.
3.x -4,或x
-4,或x 3.
3.
(课本第21页)练习1-3.
答案:1.⑴{x|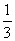 <x<2};⑵{x|x
<x<2};⑵{x|x
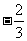 ,或x
,或x
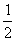 };⑶φ;⑷ R.
};⑶φ;⑷ R.
2.⑴x=2-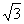 ,或x=2+
,或x=2+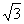 ;⑵x<2-
;⑵x<2-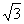 ,或x>2+
,或x>2+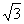 ;⑶2-
;⑶2-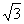 <x<2+
<x<2+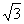 .
.
例1 (课本第19页)解不等式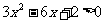
解:作出函数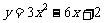 的图像
的图像
因为 .
.
所以,原不等式的解集是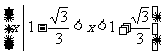 .
.
例2 (课本第20页)解不等式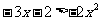 .
.
解:整理得 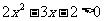
因为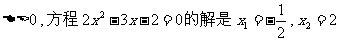 .
.
所以,原不等式的解集是 .
.
例3 (课本第20页)解不等式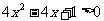 .
.
解:因为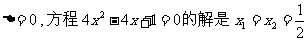 .
.
所以,原不等式的解集是 .
.
例4 (课本第20页)解不等式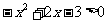 .
.
解:整理,得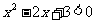 .
.
因为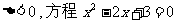 无实数解,
无实数解,
所以不等式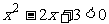 的解集是
的解集是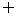 .
.
从而,原不等式的解集是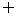 .
.
4.像3x-15>0(或<0)这样的不等式,常用的有两种解法 (1)图象解法:利用一次函数y=3x-15的图象求解
(1)图象解法:利用一次函数y=3x-15的图象求解 注:①直线与x轴交点的横坐标,就是对应的一元一次方程的根
注:①直线与x轴交点的横坐标,就是对应的一元一次方程的根 ②图象在x轴上面的部分表示3x-15>0
②图象在x轴上面的部分表示3x-15>0 (2)代数解法:用不等式的三条基本性质直接求解
(2)代数解法:用不等式的三条基本性质直接求解 注 这个方法也是对比一元一次方程的解法得到的
注 这个方法也是对比一元一次方程的解法得到的 二、讲解新课:
二、讲解新课:
画出函数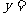
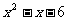 的图象,利用图象回答:
(1)方程
的图象,利用图象回答:
(1)方程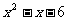 =0的解是什么;
(2)x取什么值时,函数值大于0;
(3)x取什么值时,函数值小于0
=0的解是什么;
(2)x取什么值时,函数值大于0;
(3)x取什么值时,函数值小于0 (这也是初中作过的题目)
结合二次函数
(这也是初中作过的题目)
结合二次函数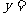
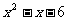 的对应值表与图象(表、图略),可以得出,方程
的对应值表与图象(表、图略),可以得出,方程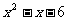 =0的解是x=-2,或x=3;
当x<-2,或x>3时,y>0,即
=0的解是x=-2,或x=3;
当x<-2,或x>3时,y>0,即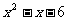 >0;
当-2<x< 3时,y< 0,即
>0;
当-2<x< 3时,y< 0,即 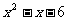 <0
<0 经上结果表明,由一元二次方程数
经上结果表明,由一元二次方程数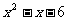 =0的解是x=-2,或 x=3,结合二次函数
=0的解是x=-2,或 x=3,结合二次函数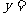
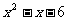 图象,就可以知道一元二次不等式
图象,就可以知道一元二次不等式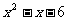 >0的解集是{x|x<-2,或x>3};一元二次不等式
>0的解集是{x|x<-2,或x>3};一元二次不等式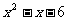 <0的解集是{x|-2<x<3}
<0的解集是{x|-2<x<3} 一般地,怎样确定一元二次不等式
一般地,怎样确定一元二次不等式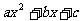 >0与
>0与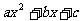 <0的解集呢?
组织讨论:
从上面的例子出发,综合学生的意见,可以归纳出确定一元二次不等式的解集,关键要考虑以下两点:
(1)抛物线
<0的解集呢?
组织讨论:
从上面的例子出发,综合学生的意见,可以归纳出确定一元二次不等式的解集,关键要考虑以下两点:
(1)抛物线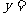
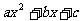 与x轴的相关位置的情况,也就是一元二次方程
与x轴的相关位置的情况,也就是一元二次方程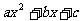 =0的根的情况
(2)抛物线
=0的根的情况
(2)抛物线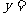
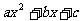 的开口方向,也就是a的符号
的开口方向,也就是a的符号 总结讨论结果:
(l)抛物线
总结讨论结果:
(l)抛物线 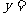
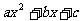 (a> 0)与 x轴的相关位置,分为三种情况,这可以由一元二次方程
(a> 0)与 x轴的相关位置,分为三种情况,这可以由一元二次方程 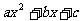 =0的判别式
=0的判别式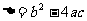 三种取值情况(Δ> 0,Δ=0,Δ<0)来确定
三种取值情况(Δ> 0,Δ=0,Δ<0)来确定 因此,要分二种情况讨论
因此,要分二种情况讨论 (2)a<0可以转化为a>0
(2)a<0可以转化为a>0 分Δ>O,Δ=0,Δ<0三种情况,得到一元二次不等式
分Δ>O,Δ=0,Δ<0三种情况,得到一元二次不等式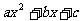 >0与
>0与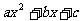 <0的解集
<0的解集
一元二次不等式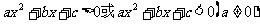 的解集:
的解集:
设相应的一元二次方程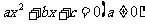 的两根为
的两根为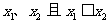 ,
,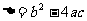 ,则不等式的解的各种情况如下表:(课本第19页)
,则不等式的解的各种情况如下表:(课本第19页)
|
|
 |
 |
 |
|
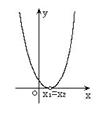
二次函数 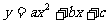 (  )的图象 )的图象 |
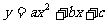 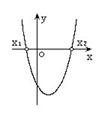 |
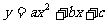  |
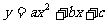 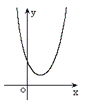 |
一元二次方程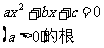 |
有两相异实根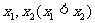 |
有两相等实根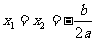 |
无实根 |
 |
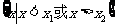 |
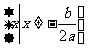 |
R |
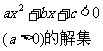 |
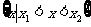 |
 |
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com