
3.已知直线l过A(-2,(t+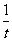 )2)、B(2,(t-
)2)、B(2,(t-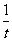 )2)两点,则此直线斜率为 ,倾斜角为___
)2)两点,则此直线斜率为 ,倾斜角为___ 
2.已知直线l1的倾斜角为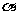 1,则l1关于x轴对称的直线l2的倾斜角
1,则l1关于x轴对称的直线l2的倾斜角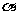 2为________.
2为________.
1.若直线 过(-2,3)和(6,-5)两点,则直线
过(-2,3)和(6,-5)两点,则直线 的斜率为 ,倾斜角为
的斜率为 ,倾斜角为
例1求经过A(-2,0)、B(-5,3)两点的直线的斜率和倾斜角.
解: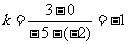 ,就是
,就是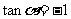
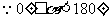
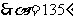
因此,这条直线的斜率是-1,倾斜角是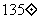
点评:此题要求学生会通过斜率公式求斜率,并根据斜率求直线的倾斜角.
例2求过下列两点的直线的斜率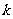 及倾斜角
及倾斜角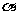
①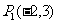 、
、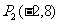 ;
斜率不存在,
;
斜率不存在,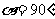
②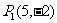 、
、 ;
;
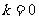 ,
,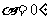
③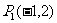 、
、
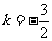 ,
,
点评:结合反三角的知识写出斜率在不同取值范围内所对应的倾斜角表
达式:①当 时,
时,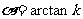 ;②当
;②当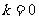 时,
时,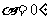 ;
;
③当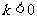 时,
时,

例3 若三点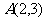 ,
,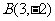 ,
,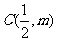 共线,求
共线,求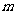 的值
的值
解: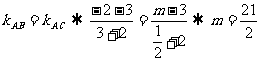

拓广:到目前为止共有几种证明三点共线的方法
例4 已知三角形的顶点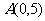 ,
,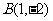 ,
,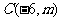 ,
,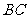 中点为
中点为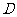 ,当
,当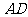 的斜率为1时,求
的斜率为1时,求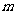 的值及
的值及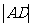 的长
的长
解: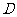 点坐标为
点坐标为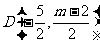 ,
,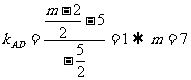

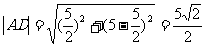

6.确定一条直线需要具备几个独立条件:需要知道直线经过两个已知点;需要知道直线经过一个已知点及方向(即斜率)等等
5.斜率公式的形式特点及适用范围:
①斜率公式与两点的顺序无关,即两点的纵坐标和横坐标在公式中的前后次序可同时颠倒;
②斜率公式表明,直线对于x轴的倾斜程度,可以通过直线上任意两点坐标表示,而不需求出直线的倾斜角;
③斜率公式是研究直线方程各种形式的基础,必须熟记,并且会灵活运用;
④当 时,直线的倾斜角
时,直线的倾斜角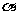 =
=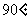 ,没有斜率
,没有斜率
4.斜率公式:经过两点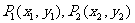 的直线的斜率公式:
的直线的斜率公式:
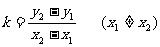

推导:设直线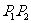 的倾斜角是
的倾斜角是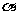 ,斜率是
,斜率是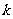 ,向量
,向量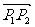 的方向是向上的(如上图所示).向量
的方向是向上的(如上图所示).向量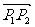 的坐标是
的坐标是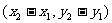 .过原点作向量
.过原点作向量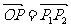 ,则点P的坐标是
,则点P的坐标是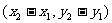 ,而且直线OP的倾斜角也是
,而且直线OP的倾斜角也是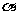 ,根据正切函数的定义,
,根据正切函数的定义,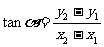
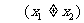
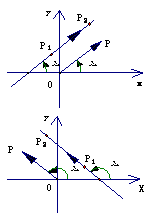 即
即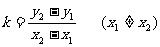

同样,当向量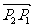 的方向向上时也有同样的结论.
的方向向上时也有同样的结论.
当 (即直线和x轴垂直)时,直线的倾斜角
(即直线和x轴垂直)时,直线的倾斜角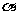 =
=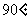 ,没有斜率
,没有斜率
3.概念辨析:①当直线和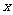 轴平行或重合时,规定直线的倾斜角为0°;②直线倾斜角的取值范围是0°≤
轴平行或重合时,规定直线的倾斜角为0°;②直线倾斜角的取值范围是0°≤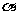 <180°;③倾斜角是90°的直线没有斜率.
<180°;③倾斜角是90°的直线没有斜率.
提问:
⑴哪些条件可以确定一条直线?
⑵在平面直角坐标系中,过点P的任何一条直线 ,对
,对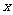 轴的位置有哪些情形?如何刻划它们的相对位置?
轴的位置有哪些情形?如何刻划它们的相对位置?
⑶给定直线的倾斜角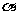 ,如何求斜率?
,如何求斜率?
⑷设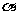 是直线的倾斜角,
是直线的倾斜角,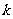 为其斜率,则当
为其斜率,则当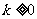 及
及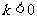 时,与之相应的
时,与之相应的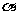 取值范围是什么
取值范围是什么
⑸判断正误:
①直线的倾斜角为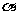 ,则直线的斜率为
,则直线的斜率为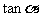 ( )
( )
②直线的斜率值为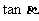 ,则它的倾斜角为
,则它的倾斜角为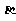 ( )
( )
③因为所有直线都有倾斜角,故所以直线都有斜率( )
④因为平行于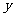 轴的直线的斜率不存在,所以平行于
轴的直线的斜率不存在,所以平行于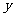 轴的直线的倾斜角不存在 ( )
轴的直线的倾斜角不存在 ( )
2.直线的倾斜角与斜率:在平面直角坐标系中,对于一条与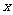 轴相交的直线,如果把
轴相交的直线,如果把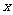 轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为
轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为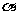 ,那么
,那么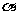 就叫做直线的倾斜角.当直线和
就叫做直线的倾斜角.当直线和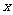 轴平行或重合时,我们规定直线的倾斜角为0°.
轴平行或重合时,我们规定直线的倾斜角为0°.
倾斜角的取值范围是0°≤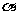 <180°.倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率,常用
<180°.倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率,常用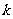 表示.
表示.
1.直线方程的概念:以一个方程的解为坐标的点都是某条直线上的点,反过来,这条直线上的点的坐标都是这个方程的解,这时,这个方程就叫做这条直线的方程,这条直线叫做这个方程的直线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com