
2. 库仑定律: 在真空中的两个点电荷间的相互作用力,跟它们电量的乘积成正比,跟它们距离的平方成反比,作用力的方向在它们的连线上。
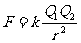
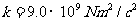
例:已知两个固定点电荷,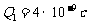
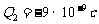 ,它们之间的距离为20厘米,引入第三个点电荷(1)若使
,它们之间的距离为20厘米,引入第三个点电荷(1)若使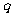 静止?求其所放位置、电量、电性(2)若
静止?求其所放位置、电量、电性(2)若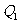
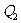 都为自由点电荷,放入第三个点电荷均平衡,求
都为自由点电荷,放入第三个点电荷均平衡,求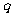 的电性;
的电性;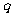 的位置;
的位置;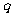 的电量。
的电量。
小结:真空的三个自由点电荷达平衡时的特点:
(1) 三点共线,两同夹异,两大夹小。
(2) 第三者靠近原来电量较小的,由它的受力平衡求间距;
(3) 由前两者电量的平衡求第三个点电荷的电量。
1. 电荷守恒定律:电荷既不会创生,也不会消失,它只能从一个物体上(或某一部分)转移到另一物体(或部分),而电荷的总量保持不变。
6.在平面内,先将一个多边形以点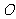 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为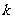 ,并且原多边形上的任一点
,并且原多边形上的任一点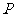 ,它的对应点
,它的对应点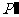 在线段
在线段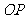 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点
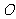 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为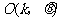 ,其中点
,其中点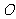 叫做旋转相似中心,
叫做旋转相似中心,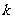 叫做相似比,
叫做相似比, 叫做旋转角.
叫做旋转角.
(1)填空:
①如图1,将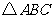 以点
以点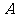 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转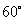 ,得到
,得到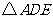 ,这个旋转相似变换记为
,这个旋转相似变换记为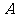 ( , );
( , );
②如图2,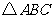 是边长为
是边长为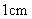 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换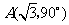 ,得到
,得到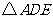 ,则线段
,则线段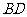 的长为
的长为 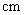 ;
;
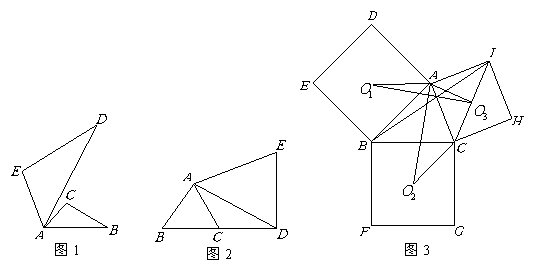 (2)如图3,分别以锐角三角形
(2)如图3,分别以锐角三角形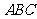 的三边
的三边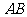 ,
,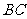 ,
,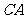 为边向外作正方形
为边向外作正方形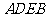 ,
,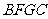 ,
,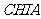 ,点
,点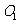 ,
, ,
,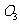 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用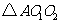 与
与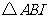 ,
,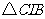 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段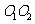 与
与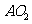 之间的关系.
之间的关系.
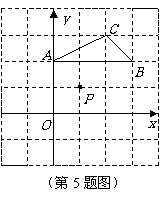
5.如图,在平面直角坐标系中,点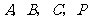 的坐标分别为
的坐标分别为
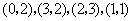 .
.
(1)请在图中画出 ,使得
,使得 与
与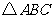 关于点
关于点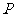 成中心对称;
成中心对称;
(2)若一个二次函数的图象经过(1)中 的三个顶点,求此二次函数的关系式.
的三个顶点,求此二次函数的关系式.
4.如图,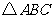 中
中 ,
,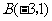 ,
,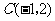 .
.
(1)将 向右平移
向右平移 个单位长度,
个单位长度,
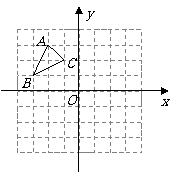 画出平移后的
画出平移后的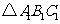 ;
;
(2)画出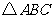 关于
关于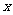 轴对称的
轴对称的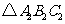 ;
;
(3)将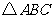 绕原点
绕原点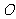 旋转
旋转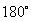 ,画出旋转后的
,画出旋转后的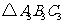 ;
;
(4)在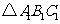 ,
,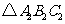 ,
,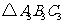 中,
中,
 ______与
______与 ______成轴对称,对称轴是______;
______成轴对称,对称轴是______;
 ______与
______与 ______成中心对称,对称中心的坐标是______.
______成中心对称,对称中心的坐标是______.
3.在平面直角坐标系中,直线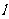 过点M(3,0),且平行于
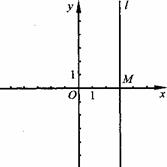
过点M(3,0),且平行于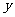 轴.
轴.
 (1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-l,O),C(-1,2),△ABC关于
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-l,O),C(-1,2),△ABC关于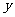 轴的对称图形是△A1B1C1,△A1B1C1关于直线
轴的对称图形是△A1B1C1,△A1B1C1关于直线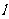 的对称
的对称
图形是△A2B2C1,写出△A2B2C1的三个顶点的坐标;
(2)如果点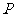 的坐标是(
的坐标是( ,0),其中
,0),其中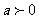 ,点P关于
,点P关于
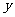 轴的对称点是
轴的对称点是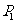 ,点
,点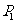 关于直线
关于直线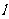 的对称点是
的对称点是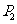 ,
,
求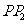 的长.
的长.
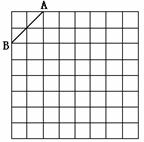
2.如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
⑴ 请在网格中建立平面直角坐标系, 使A点坐标为(-2,4),B点坐标为(-4,2);
⑵ 在第二象限内的格点上画一点C, 使点C与线段AB组成一个以AB为底的等腰三角形, 且腰长是无理数, 则C点坐标是 , △ABC的周长是 (结果保留根号);
⑶ 画出△ABC以点C为旋转中心、旋转180°后的△A′B′C, 连结AB′和A′B, 试说出四边形ABA′B′是何特殊四边形, 并说明理由.
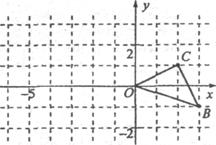
1.如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).
(1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)分别写出B、C两点的对应点B′、C′的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.
6.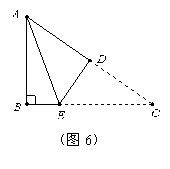 如图6,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长等于_________cm.
如图6,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长等于_________cm.
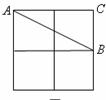
5.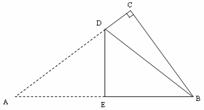 如图5,在
如图5,在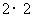 的正方形格纸中,有一个以格点为顶点的
的正方形格纸中,有一个以格点为顶点的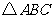 ,请你找出格纸中所有与
,请你找出格纸中所有与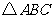 成轴对称且也以格点为顶点的三角形,这样的三角形共有 个.
成轴对称且也以格点为顶点的三角形,这样的三角形共有 个.
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com