
26.(本小题满分14分)在图1--3中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=2b,且边AD和AE在同一直线上.
(1)操作发现:
①当2b<a时,如图1,在BA上选取点G,使BG=b,连结FG和CG,裁掉△FAG和△CGB,小明发现:如果先将△FAG绕点F逆时针旋转90°到△FEH的位置,那么△CGB恰可以拼接到△CHD的位置.请说明理由.
 ②对于拼接成的新四边形FGCH,小明通过度量发现其恰是正方形.请说明理由.
②对于拼接成的新四边形FGCH,小明通过度量发现其恰是正方形.请说明理由.
(2)实践探究:小明进一步探究后发现:当2b<a 、2b=a、a<2b<2a、b=a时(即b≤a时),此类图形都能剪拼成正方形,且所选取的点G的位置在BA方向上随着b的增大不断上移.请你类比图1的剪拼方法,在图2(a<2b<2a)中画出剪拼成一个新正方形的示意图.
(3)联想拓展:当b>a时,如图3的图形能否剪拼成一个正方形?若能,请你在图中画出剪拼的示意图;若不能,简要说明理由.
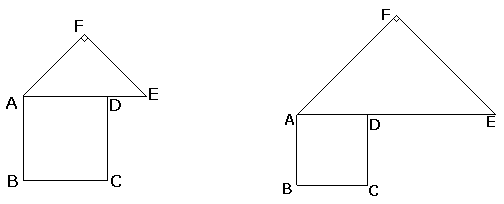
图2(a<2b<2a) 图3(b>a)
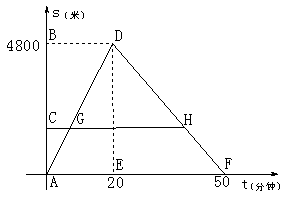
25.(本小题满分12分)为宣传“09连云港之夏--连岛旅游度假区”,连云港电视台摄制组乘船往返于大沙湾(A)、苏马湾(B)两码头(假设船速、海水从大沙湾流向苏马湾的速度都为定值),在A、B间设立拍摄中心C,拍摄黄海之滨沿岸的景色.往返过程中,船在C、B处均不停留,离开码头A的距离s(米)与航行的时间t(分钟)之间的函数关系如图所示.根据图象提供的信息,解答下列问题:
(1)船只从码头A→B,航行的时间为 分钟、航行的速度为 米/分钟;船只从码头B→A,航行的时间为 分钟、航行的速度为 米/分钟.
(2)过点C作CH∥t轴,分别交AD、DF于点G、H,设AC= ,GH=
,GH=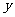 ,求出
,求出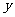 与
与 之间的函数关系式.
之间的函数关系式.
(3)若拍摄中心C设在离A码头1600米处, 摄制组在拍摄中心C分两组行动,一组乘橡皮艇顺水漂流而下,另一组乘船到达码头B后,立即返回.
摄制组在拍摄中心C分两组行动,一组乘橡皮艇顺水漂流而下,另一组乘船到达码头B后,立即返回.
①求船只往返C、B两处所用的时间.
②两组在途中相遇,求相遇时船只离拍摄中心C有多远.
24.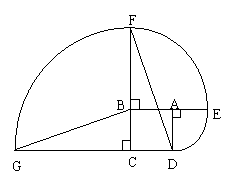 (本小题满分10分)如图,ABCD是边长为1的正方形,其中弧DE、弧EF、弧FG的圆心依次是A、B、C.
(本小题满分10分)如图,ABCD是边长为1的正方形,其中弧DE、弧EF、弧FG的圆心依次是A、B、C.
(1)求点D沿三条圆弧运动到点G所经过的路线长;
(2)判断直线GB与DF的位置关系,并说明理由.
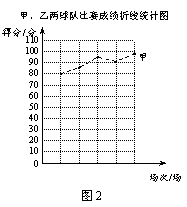
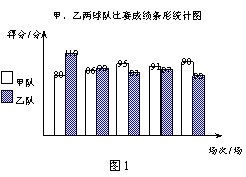
23.(本小题满分10分)甲、乙两支篮球队在集训期内进行了五场比赛,将比赛成绩进行统计后,绘制成如图1、图2的统计图.
(1)在图2中画出折线表示乙队在集训期内这五场比赛成绩的变化情况;
(2)已知甲队五场比赛成绩的平均分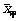 =90分,请你计算乙队五场比赛成绩的平均分
=90分,请你计算乙队五场比赛成绩的平均分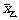 ;
;
(3)就这五场比赛,分别计算两队成绩的极差;


 (4)如果从甲、乙两队中选派一支球队参加篮球锦标赛,根据上述统计,从平均分、折线的走势、获胜场数和极差四个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
(4)如果从甲、乙两队中选派一支球队参加篮球锦标赛,根据上述统计,从平均分、折线的走势、获胜场数和极差四个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
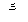

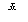
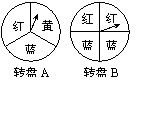
22.(本小题满分10分)如图,有两个可以自由转动的均匀转盘,转盘A被分成面积相等的三个扇形,转盘B被分成面积相等的四个扇形,每个扇形内都涂有颜色.同时转动两个转盘,停止转动后,若一个转盘的指针指向红色,另一个转盘的指针指向蓝色,则配成紫色;若其中一个指针指向分界线时,需重新转动两个转盘.
(1)用列表或画树状图的方法,求同时转动一次转盘A、B配成紫色的概率;
(2)小强和小丽要用这两个转盘做游戏,他们想出如下两种游戏规则:
①转动两个转盘,停止后配成紫色,小强获胜;否则小丽获胜;
②转动两个转盘,停止后指针都指向红色,小强获胜;指针都指向蓝色,小丽获胜.
 判断以上两种规则的公平性,并说明理由.
判断以上两种规则的公平性,并说明理由.
21.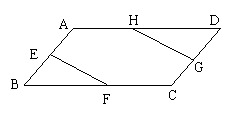 (本小题满分8分)如图,点E、F、G、H分别是平行四边形ABCD的边AB、BC、CD、DA的中点.
(本小题满分8分)如图,点E、F、G、H分别是平行四边形ABCD的边AB、BC、CD、DA的中点.
求证:△BEF≌△DGH.
20.(本小题满分12分)小明在复习数学知识时,针对“求一元二次方程的解”,整理了以下的几种方法,请你按有关内容补充完整.
举例:求一元二次方程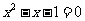 的两个解.
的两个解.
方法一:选择一种合适的方法(配方法、公式法、因式分解法)求解.
解方程: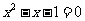 .
.
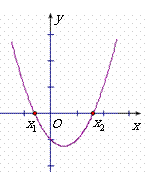
方法二:利用二次函数图象与坐标轴的交点求解.如图所示,
把方程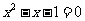 的解看成是二次函数
的解看成是二次函数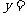
的图象与 轴交点的横坐标,即
轴交点的横坐标,即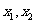 就是方程的解.
就是方程的解.
方法三:利用两个函数图象的交点求解.
(1)把方程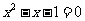 的解看成是一个二次函数
的解看成是一个二次函数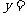 的图象与一个一次函数
的图象与一个一次函数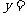 图象交点的横坐标;
图象交点的横坐标;
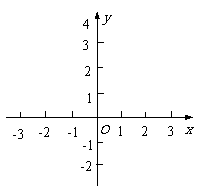 (2)画出这两个函数的图象,用
(2)画出这两个函数的图象,用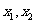 在
在 轴上标出方程的解.
轴上标出方程的解.
19.(本小题满分6分)计算: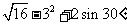
18.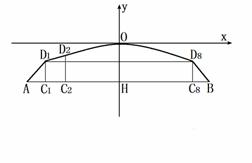 如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1
和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4 米,点D2的坐标为(
如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1
和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4 米,点D2的坐标为( 13,
13, 1.69),则桥架的拱高OH=
米.
1.69),则桥架的拱高OH=
米.

17.根据下列图形的排列规律,第2008个图形
是 (填序号即可). (①†;②‡;③‰;④ˆ)
‡†‰ˆˆ‡†‰ˆ‡‡†‰ˆˆ‡……
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com