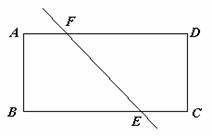
18、如图，直线EF将矩形纸片ABCD分成面积相等的两部分，E、F分别与BC交于点E，与AD交于点F(E，F不与顶点重合)，设AB=a,AD=b,BE=x．

(Ⅰ)求证：AF=EC；

(Ⅱ)用剪刀将纸片沿直线EF剪开后，再将纸片ABEF沿AB对称翻折，然后平移拼接在梯形ECDF的下方，使一底边重合，直腰落在边DC的延长线上，拼接后，下方的梯形记作EE′B′C.

　 (1)求出直线EE′分别经过原矩形的顶点A和顶点D时，所对应的 x：b的值；

　 (2)在直线EE′经过原矩形的一个顶点的情形下，连接BE′，直线BE′与EF是否平行？你若认为平行，请给予证明；你若认为不平行，请你说明当a与b满足什么关系时，它们垂直？

命题意图：选题的目的是我觉得近几年南京市的中考题中的压轴题很喜欢考这种将几何图形进行翻折、平移等变换来探索结论，且让学生自己画出符合题意的图形，学生受思维能力与空间想象力的限制，很难理解题意。

参考答案：(Ⅰ)证明：∵AB=a，AD=b，BE=x ，S_梯形ABEF= S_梯形CDFE．

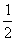∴a(x+AF)=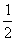a(EC+b-AF)，

∴2AF=EC+(b-x)．

又∵EC＝b-x，

∴2AF=2EC，即AF=EC；

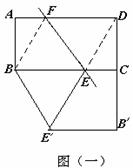　(Ⅱ)(1)当直线EE′经过原矩形的顶点D时，如图(一)，

∵EC∥E′B′，

∴=.

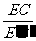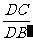由EC＝b-x，E′B′=EB=x， DB′=DC+CB′=2a，

得，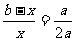

∴x：b= _；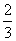

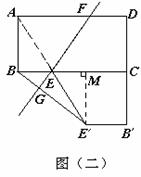
当直线E′E经过原矩形的顶点A时，如图(二)，

在梯形AE′B′D中，

∵EC∥E′B′,点C是DB′的中点，

∴CE=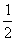(AD+ E′B′)，

即b-x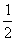＝(b+x)，

∴x：b=．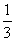

(2) 如图(一)， 当直线EE′ 经过原矩形的顶点D时，BE′∥EF．

证明：连接BF．

∵FD∥BE, FD=BE，

∴四边形FBED是平行四边形，

∴FB∥DE， FB=DE,

又∵EC∥E′B′， 点C是DB′的中点，

∴DE=EE′，

∴FB∥EE′, FB= EE′，

∴四边形BE′EF是平行四边形

∴BE′∥EF．

如图(二)， 当直线EE′ 经过原矩形的顶点A时，显然BE′与EF不平行，设直线EF与BE′交于点G.过点E′作E′M⊥BC于M， 则E′M=a.．

∵x：b=，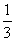

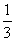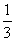∴EM=BC=b．

若BE′与EF垂直，则有∠GBE+∠BEG=90°

又∵∠BEG＝∠FEC＝∠MEE′， ∠MEE′+∠ME′E=90°，

∴∠GBE=∠ME′E.

Rt△BME′中，tan∠E′BM= tan∠GBE==．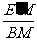

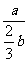在Rt△EME′中，tan∠ME′E ==，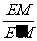

∴＝．

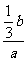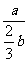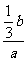又∵a＞0，b＞0，

，

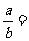
∴当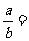时，BE′与EF垂直.

试题来源：2007年山东省临沂市初中毕业与高中招生考试

17、容积率t是指在房地产开发中建筑面积与用地面积之比，为充分利用土地资源，更好地解决人们的住房需求，并适当的控制建筑物的高度，一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时，结合往年开发经验知，建筑面积M(m²)与容积率t的关系可近似地用如图(1)中的线段l来表示；1 m²建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示．

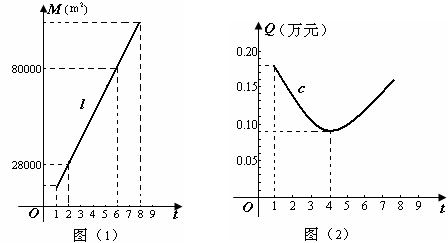
(1)试求图(1)中线段l的函数关系式，并求出开发该小区的用地面积；

(2)求出图(2)中抛物线段c的函数关系式.

命题意图:我觉得近几年南京市的中考题在倒数第二题都是考查生活中的实际问题，且题干长，题意不容易理解，而且经常与二次函数相联系。

参考答案：(Ⅰ)设线段l函数关系式为M=kt+b，由图象得

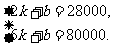
解之，得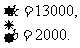

∴线段l的函数关系式为M＝13000t+2000,　 1≤t≤8.由t=知，当t=1时，S_用地面积=M_建筑面积，

把t=1代入M＝13000t+2000中，得M=15000 m².

即开发该小区的用地面积是15000 m².

(Ⅱ)根据图象特征可设抛物线段c的函数关系式为Q＝a( t－4)²+k, 把点(4,0.09), (1,0.18)代入，得

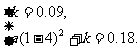
解之，得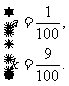

∴抛物线段c的函数关系式为 Q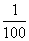＝( t－4)²+,

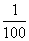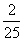即Q＝t²-t +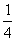,　 1≤t≤8.

试题来源：2007年日照市中等学校统一招生考试

16、某工程机械厂根据市场需求，计划生产A、B两种型号的大型挖掘机共100台，该厂所筹生产资金不少于22400万元，但不超过22500万元，且所筹资金全部用于生产此两型挖掘机，所生产的此两型挖掘机可全部售出，此两型挖掘机的生产成本和售价如下表：

(1)该厂对这两型挖掘机有哪几种生产方案？

(2)该厂如何生产能获得最大利润？

(3)根据市场调查，每台B型挖掘机的售价不会改变，每台A型挖掘机的售价将会提高m万元(m＞0)，该厂应该如何生产可以获得最大利润？(注：利润＝售价－成本)

命题意图：考查学生解决实际问题的能力，试题的特色是在要求学生能读懂题意，并且会用函数知识去解题，以及会讨论函数的最大值。

参考答案：(1) 设生产A种型号的大型挖掘机x台，则生产B种型号的大型挖掘机(100-x)台。

　　　　　　　 则22400200x+240(100-x) 22500

　　　　　　　 解得：37.5x40

　　　　　　　 X可以取38、39、40

　　　　 (2)　 设最大利润是w元

　　　　　　　 则w=50x+60(100-x)=6000-10x，当x=38 时，w有最大值。

　　　　 (3)　 因为w=(50+m)x+60(100-x)=6000+( m-10)x

　　　　　　　 则当0<m<10,x=38, w最大

　　　　　　　 当m=10,三个方案都一样。

　　　　　　　 当m>10，x=40, w最大.

试题来源：2007年山东省临沂市初中毕业与高中招生考试

15、在一次促销活动中，某商场为了吸引顾客，设立了一个可以自由转动的

转盘(如图，转盘被平均分成16份)，并规定：顾客每购买100元的商品，

就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红色、黄

色、绿色区域，那么顾客就可以分别获得50元、30元、20元的购物券，

凭购物券可以在该商场继续购物．如果顾客不愿意转转盘，那么可以直接

获得购物券10元．

(1)求每转动一次转盘所获购物券金额的平均数；

(2)如果你在该商场消费125元，你会选择转转盘还是直接获得购物券？说明理由．

命题意图：考查的目的是考查学生对于概率知识的掌握，试题的特色是答案是开放型答案，题目的核心是考查学生对于平均水平的理解。

参考答案：：⑴ 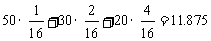　(元)；　

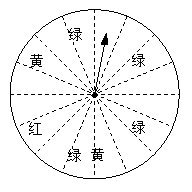⑵ 　∵11.875元＞10元，

∴选择转转盘． (如果学生选择直接获得购物券，

只要回答合理即可同样得分)

试题来源：2007年青岛市中等学校招生考试

14、灌云县实验中学为了解毕业年级800名学生每学期参加社会实践活动的时间，随机对该年级60名学生每学期参加社会实践活动的时间进行了统计，结果如下表：

分组	频数	频率
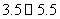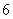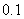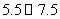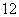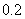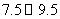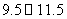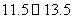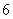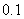合计

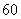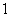(1)补全右面的频率分布表；

(2)请你估算这所学校该年级的学生中，每学期参加社会实践活动的时间大于7天的约有多少人？

命题意图：考查学生对于统计知识的掌握，试题的特色是与学生平时的生活密切相关。

参考答案：(1)，，；，，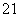

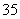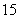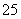
(2)

试题来源：2007年泰安市中等学校招生考试

13、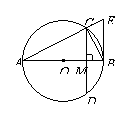如图，AB为⊙O的直径，弦CD⊥AB于点M，过点B作BE∥CD，交AC的延长

线于点E，连结BC。

(1)求证：BE为⊙O的切线；

(2)如果CD＝6，tan∠BCD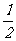＝，求⊙O的直径。

命题意图：考查的目的是考查学生对圆、三角函数、以及

说理能力。

参考答案：

(1)∵BE∥CD，AB⊥CD

　∴AB⊥CD。

∵AB是⊙O的直径

∴BE为⊙O的切线

　(2)∵AB是⊙O的直径，AB⊥CD

　　　 ∴CM= 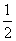CD，弧BC=弧BD

　　　 ∴∠BAC=∠BCD

∵tan∠BCD=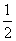

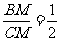
∴BM=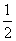CM=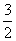

∴=

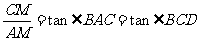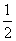
∴AM=6

∴AB=7.5

试题来源：2007年山东省济宁市中等学校招生考试

12、如图①是一个美丽的风车图案，你知道它是怎样画出来的吗？按下列步骤可

画出这个风车图案：在图②中，先画线段OA，将线段OA平移至CB处，得到风

车的第一个叶片F₁，然后将第一个叶片OABC绕点O逆时针旋转180°得到第二

个叶片F₂，再将F₁、F₂同时绕点O逆时针旋转90°得到第三、第四个叶片F₃、F₄。

根据以上过程，解答下列问题：

(1)若点A的坐标为(4，0)，点C的坐标为(2，1)，写出此时点B的坐标；

(2)请你在图②中画出第二个叶片F₂；

(3)在(1)的条件下，连接OB，由第一个叶片逆时针旋转180°得到第二个叶片的过程中，线段OB扫过的图形面积是多少？

命题意图：考查学生对于坐标系中对称图形的

作图等能力。

参考答案：(1)B(6，1)(2)图略(3)

线段OB扫过的图形为半圆，过B作BD⊥x轴

于点D，由(1)可知B(6，1)，可知OB的平方为

37，所以线段OB扫过的图形面积是18.5π。

试题来源：

2007年武汉市新课程初中毕业生学业考试

11、灌云向阳路边蔬菜批发市场上有以下信息内容：

张大爷共用325元钱从蔬菜批发市场上批发了黄瓜和西红柿共120公斤到菜市场去卖，当天上午卖完。

(1)请你计算出张大爷赚了多少钱？

(2)张大爷用300 元钱批发哪种蔬菜赚钱最多？

命题意图：考查学生对用列方程组解决实际问题的能力，试题的特色是在考查学生对实际生活的了解。

参考答案：85元

试题来源：自创

10、解方程：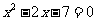

命题意图：考查学生解一元二次方程的能力，且方法多样，可灵活选择。

参考答案：

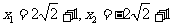
试题来源：自创

9、先化简，再求值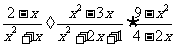：，其中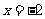

命题意图：考查学生基本的因式分解、分式计算、与代数式求值。

参考答案：

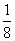
试题来源：自创