
7.二项式定理: ;
;
二项展开式的通项公式:
 .
.
[题例分析]
例1、从6名短跑运动员中选4人参加4×100米接力,如果其中甲不跑第一棒,乙不跑第四棒,问共有多少种参赛方法?
解法:问题分成三类:(1)甲乙二人均不参加,有 种;(2)甲、乙二人有且仅有1人参加,有2
种;(2)甲、乙二人有且仅有1人参加,有2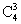 (
( -
- )种;(3)甲、乙二人均参加,有
)种;(3)甲、乙二人均参加,有 (
( -2
-2 +
+ )种,故共有252种.
)种,故共有252种.
点评:对于带有限制条件的排列、组合综合题,一般用分类讨论或间接法两种.
例2: 有5个男生和3个女生,从中选取5人担任5门不同学科的科代表,求分别符合下列条件的选法数:
(1)有女生但人数必须少于男生.
(2)某女生一定要担任语文科代表.
(3)某男生必须包括在内,但不担任数学科代表.
(4)某女生一定要担任语文科代表,某男生必须担任科代表,但不担任数学科代表.
解:(1)先取后排,有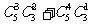 种,后排有
种,后排有 种,共有
种,共有 =5400种.
=5400种.
(2)除去该女生后先取后排: 种.
种.
(3)先取后排,但先安排该男生: 种.
种.
(4)先从除去该男生该女生的6人中选3人有 种,再安排该男生有
种,再安排该男生有 种,其余3人全排有
种,其余3人全排有 种,共
种,共 =360种.
=360种.
例3、、有6本不同的书
(1)甲、乙、丙3人每人2本,有多少种不同的分法?
(2)分成3堆,每堆2本,有多少种不同的分堆方法?
(3)分成3堆,一堆1本,一堆2本,一堆3本,有多少种不同的分堆方法?
(4)分给甲、乙、丙3人,一人1本,一人2本,一人3本,有多少不同的分配方法?
(5)分成3堆,有2堆各一本,另一堆4本,有多少种不同的分堆方法?
(6)摆在3层书架上,每层2本,有多少种不同的摆法?
解:(1)在6本书中,先取2本给甲,再从剩下的4本书中取2本给乙,最后2本给丙,共有 (种)。
(种)。
(2)6本书平均分成3堆,用上述方法重复了 倍,故共有
倍,故共有 (种)。
(种)。
(3)从6本书中,先取1本做1堆,再在剩下的5本中取2本做一堆,最后3本做一堆,共有 (种)
(种)
(4)在(3)的分堆中,甲、乙、丙3人任取一堆,故共有 (种)。
(种)。
(5)平均分堆要除以堆数的全排列数,不平均分堆则不除,故共有 (种)。
(种)。
(6)本题即为6本书放在6个位置上,共有 (种)。
(种)。
例4、如果在 的展开式中,前三项的系数成等差数列,求展开式中的有理项。
的展开式中,前三项的系数成等差数列,求展开式中的有理项。
解:展开式中前三项的系数分别为1,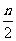 ,
,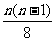 ,
,
由题意得:2×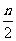 =1+
=1+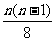 得
得 =8。
=8。
设第r+1项为有理项, ,则r是4的倍数,所以r=0,4,8。
,则r是4的倍数,所以r=0,4,8。
有理项为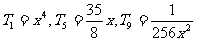 。
。
[巩固训练]
6.排列数与组合数的关系是: .
.
5.组合数的两个性质:
(1)  =
= ;
;
(2)  +
+ =
=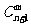
(3) .
.
4.组合数公式  =
=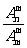 =
=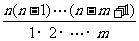 =
= (n,m∈N*,且m≤n).
(n,m∈N*,且m≤n).
3.排列数公式  =
= =
= .(n,m∈N*,且m≤n).
.(n,m∈N*,且m≤n).
2.分步计数原理(乘法原理) .
.
[基础知识]
1.分类计数原理(加法原理)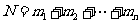 .
.
古人常使用婉辞表示特定意义,所以要注重积累这种特殊用法。
例13.先帝创业未半而中道崩殂。(《出师表》)
解析:“崩殂”是帝王死的委婉说法。
例14.仆赖无人绪业,得待罪辇毂下,二十余年矣。(《报任少卿书》)
解析:“待罪”是做官的谦词。
(源自《语文报·高中版》2009年第24期)
文言文中一些貌似现代汉语中的双音词,其实是古汉语中两个单音节词的连用。它们同形异义,极易误解,要具体情况具体分析。
例11.乃不知有汉,无论魏晋。(《桃花源记》)
解析:无,不要;论,说;无论,不要说。和现代汉语“无论”有别。
例12.中间力拉崩倒之声。(《口技》)
解析:中,里面;间,夹杂;中间,中间夹杂。区别于现代汉语“中间”。
指在本义或引申义解释不通的情况下,试着找通假字,从而解释出符合语境的意思。
例9.便要还家,设酒杀鸡作食。(《桃花源记》)
解析:“要”与“邀”同音通假,“要”解释为“邀请”。
例10.政通人和,百废具兴。(《岳阳楼记》)
解析:“具”通“俱”,都。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com