
3、袋内装有10个相同的球,其中5个球标有数字0,5个球标有数字1,若从袋中摸出5个球,那么摸出的5个球所标数字之和小于2或大于3的概率是 .
2、将一颗质地均匀的骰子(它是一种各面上分别标有点数1,2,3,4,5,6的正方体玩具)先后抛掷3次,至少出现一次6点向上和概率是
(A) (B) (C) (D)
1、数字1,2,3,4,5,中,随机抽取3个数字(允许重复)组成一个三位数,其各位数字之和等于9的概率为( )

[基础知识]
等可能性事件的概率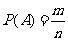 .
.
[题例分析]
例1、 某班有学生36人,血型分别为A型12人,B型10人,AB型8人,O型6人,现从中抽出2人,求这两人血型不相同的概率.
解:P(两人血型相同)=P(两人血型均为A型)+P(两人血型均为B型)+P(两人血型均为AB型)+P(两人血型均为O型)=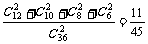 .
.
所以,P(两人血型不同)=1-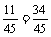 .
.
点拨:从四种血型中抽出2种有C24=6种,依次分类则情形较复杂,所以本题用间接法较简便.
例2、从男、女学生共有36名的班级中,任意选出两名委员,任何人都有同样的机会当选,如果选得同性委员的概率等于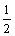 ,求男、女相差几名?
,求男、女相差几名?
解:设男生有x名,则女生有36-x名,选得2名委员都是男性的概率为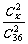 =
=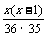 .选得两名委员都是女性的概率为
.选得两名委员都是女性的概率为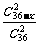 =
=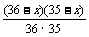 .
.
以上两种选法是互斥的,所以选得两名委员是同性委员的概率等于其概率和.
依题意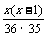 +
+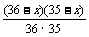 =
=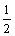 .解得x=15或x=21.
.解得x=15或x=21.
即该班男生有15名,女生有36-15=21人或者男生有21人,女生有36-21=15人,总之,男女相差6名.
例3、在袋中装30个小球,其中彩球有n个红色,5个蓝色,10个黄色,其余为白色,求:
(1)如果已经从中取定了5个黄球和3个蓝球,并将它们编上了不同的号码后排成一排,那么使蓝色小球不相邻的排法有多少种?
(2)如果从袋中取出3个都是颜色相同的彩球(不含白色)的概率是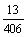 ,且n≥2,计算红球有几个?
,且n≥2,计算红球有几个?
(3)根据(2)的结论,计算从袋中任取3个小球至少有一个红球的概率?
解:(1)将5个黄球排成一排共有A55种排法,将3个蓝球放在5个黄球所形成的6个空位上,有A36种排法.∴所求的排法为A55·A36=14400(种).
(2)取3个球的种数为C330=4060,设“3个球全是红色”为事件A,“3个球全是蓝色”为事件B.“3个球都是黄色”为事件C,则P(B)=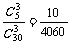 ,P(C)=
,P(C)=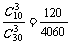 .
.
∵A、B、C彼此互斥,∴P(A+B+C)=P(A)+P(B)+P(C),
即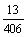 =P(A)+
=P(A)+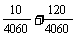 .∴P(A)=0,即取3个球,是红球的个数小于或等于2.
.∴P(A)=0,即取3个球,是红球的个数小于或等于2.
又∵n≥2,故n=2.
(3)记“3个球至少有一个是红球”为事件D,则 为“3个球中没有红球”,则
为“3个球中没有红球”,则
P(D)=1-P( )=1-
)=1- =
=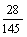 .
.
例4、一种电器控制器在出厂时每四件一等品装成一箱,工人在装箱时不小心把两件二等品和两件一等品装入一箱,为了找出该箱中的二等品,我们把该箱中产品逐一取出进行测试.
(1)求前两次取出都是二等品的概率;
(2)求第二次取出的是二等品的概率;
解:(1)四件产品逐一取出方式共有A 种不同方式.
种不同方式.
前两次取出都是二等品的方式共有A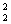 ·A
·A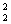 种不同方式.
种不同方式.
所以前两次取出都是二等品的概率为: 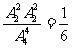 (2)第二次取出是二等品共有:
(2)第二次取出是二等品共有: ,
,
所以第二次取出是二等品的概率是: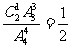
[巩固训练]
6、若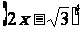 =
=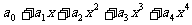 ,求(1)
,求(1)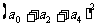 ―
―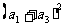 的值。(2)
的值。(2)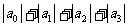 的值。
的值。
5、(1)10个优秀指标分配给6个班级,每班至少一个,共有多少种不同的分配方法?
(2)10个优秀名额分配到一、二、三3个班,若名额数不少于班级序号数,共有多少种不同的分配方法?
4、设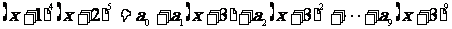
则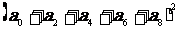 ―
―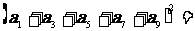
3、将标号为1,2,…,10的10个球放入标号为1,2,…,10的10个盒子内,每个盒内放一个球,则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有 种.(以数字作答)
2、某赛季足球比赛的计分规则是:胜一场,得3分;平一场,得1分;负一场,得0分.一球队打完15场,积33分.若不考虑顺序,该队胜、负、平的情况共有
A 3种 B 4种 C 5种 D 6种.
1、设k=1,2,3,4,5,则(x+2)5的展开式中xk的系数不可能是
A 10 B 40 C 50 D 80.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com