6、设每门高射炮命中飞机的概率为0.6，试求：

(1)两门高射炮同时射击一发炮弹而命中飞机的概率；

(2)若今有一飞机来犯，问需要多少门高射炮射击，才能以至少99%的概率命中它？

5、 已知甲、乙两人投篮的命中率分别为0.4和0.6．现让每人各投两次，试分别求下列事件的概率：(Ⅰ)两人都投进两球；(Ⅱ)两人至少投进三个球.

4、某健美中心对第一期60人进行减肥训练，结果40人达到减肥标准目的，按此比率，现有5人参加第二期该训练，求：至少有4人没有达到减肥目的的概率.　　　　　　　 。

3、某射手射击1次，击中目标的概率是0.9.他连续射击4次，且各次射击是否击中目标相互之间没有影响.有下列结论：

①他第3次击中目标的概率是0.9；

②他恰好击中目标3次的概率是0.9³×0.1；

③他至少击中目标1次的概率是1-0.1⁴.

其中正确结论的序号是　　　　　　 (写出所有正确结论的序号)

2、种植两株不同的花卉，它们的存活率分别为p和q，则恰有一株存活的概率为 (　　 )

(A)　 p+q－2p q 　　　　(B)　 p+q－pq　　　 (C) 　p+q　　　 (D)　 pq

1.　　 一台X型号自动机床在一小时内不需要工人照看的概率为0.8000,有四台这中型号的自动机床各自独立工作,则在一小时内至多2台机床需要工人照看的概率是 (　　 ) 　　　　　　　　　　

(A)0.1536 　 　　(B) 0.1808 　 (C) 0.5632　　　 　　 (D) 0.9728

3.(不要求记忆)n次独立重复试验中某事件恰好发生k次的概率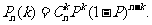

[题例分析]

例1、某产品检验员检查每一件产品时，将正品错误地鉴定为次品的概率为0.1，将次口错误地鉴定为正品的概率为0.2，如果这位检验员要鉴定4件产品，这4件产品中3件是正品，1件是次品，试求检验员鉴定成正品，次品各2件的概率.

解：有两种可能：将原1件次品仍鉴定为次品，原3件正品中1件错误地鉴定为次品;将原1件次品错误地鉴定为正品，原3件正品中的2件错误地鉴定为次品.　 概率为

P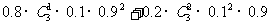＝＝0.1998

例2、已知两名射击运动员的射击水平，让他们各向目标靶射击10次，其中甲击中目标7次，乙击中目标6次，若在让甲、乙两人各自向目标靶射击3次中，求：(1)甲运动员恰好击中目标2次的概率是多少？(2)两名运动员都恰好击中目标2次的概率是多少？(结果保留两位有效数字)

解. 甲运动员向目标靶射击1次，击中目标的概率为7/10=0.7

乙运动员向目标靶射击1次，击中目标的概率为6/10=0.6

(1)甲运动员向目标靶射击3次，恰好都击中目标2次的概率是

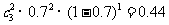
(2)乙运动员各向目标靶射击3次，恰好都击中目标2次的概率是

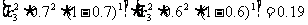
例3、冰箱中放有甲、乙两种饮料各5瓶，每次饮用时从中任意取1瓶甲种或乙种饮料，取用甲种或乙种饮料的概率相等.

(Ⅰ)求甲种饮料饮用完毕而乙种饮料还剩下3瓶的概率；

(Ⅱ)求甲种饮料被饮用瓶数比乙种饮料被饮用瓶数至少多4瓶的概率.

解：(I).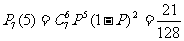　

(II)P₆(5)+P₅(5)+P₄(4) =C₆⁵P⁵(1－P)+C₅⁵P⁵+C₄⁴P⁴=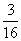

例4、有一批产品出厂前要进行五项指标检验，如果有两项指标不合格，则这批食品不能出厂，已知每项指标抽检是相互独立的，每项指标抽检出现不合格品的概率都是。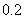

(1)求这批产品不能出厂的概率(保留三位有效数学)

(2)求直至五项指标全部检验完毕，才能确定该批产品是否出厂的概率(保留三位有效数学)

解答： (1)这批产品不能出厂的概率是：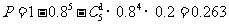

五项指标全部检验完毕，这批食品可以出厂的概率是：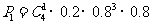

五项指标全部检验完毕，这批食品不能出厂的概率是：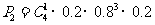

由互斥事件有一个发生的概率加法可知：五项指标全部检验完毕才能确定这批产品是否可以出厂的概率是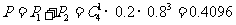

[巩固训练]

2.n个独立事件同时发生的概率 P(A₁· A₂·…· A_n)=P(A₁)· P(A₂)·…· P(A_n)．

[基础知识]

1.独立事件A，B同时发生的概率P(A·B)= P(A)·P(B).

6、掷两个骰子，出现点数之和为4点或5点或偶数点的概率是多少？