
6、解:(1)P=0.84
(2)设需要n门高射炮才能达目的,用A表示“命中飞机”这一事件,用Ai表示“第i门高射炮命中飞机”,则A1、A2…An相互独立,故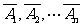 也相互独立,故P(A)=1-P(
也相互独立,故P(A)=1-P(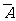 )=1-P(
)=1-P(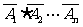 )=1-P(
)=1-P(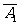 )P(
)P( )…P(
)…P( )=1-
)=1-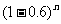 .据题意P(A)≥0.99,∴1-
.据题意P(A)≥0.99,∴1-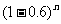 ≥99%,得n≥5.02.
≥99%,得n≥5.02.
答:至少需6门高射炮才能以99%的概率命中。
5、(Ⅰ)P(两人都投进两球)=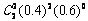
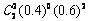 =
=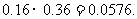
(Ⅱ)P(两人至少投进三个球)=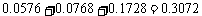
4、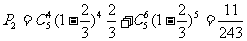
6、解:设出现4点为事件A,出现5点为事件B,出现偶数点为事C,则P(A)=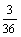 =
=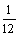 ,P(B)=
,P(B)=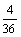 =
=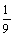 ,P(C)=
,P(C)=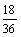 =
=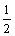 .A、B、C并非彼此互斥,4点是偶数之一,故A+C=C,而B与C互斥,∴A+B+C=B+C.
.A、B、C并非彼此互斥,4点是偶数之一,故A+C=C,而B与C互斥,∴A+B+C=B+C.
∴P(A+B+C)=P(B+C)=P(B)+P(C)=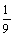 +
+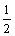 =
=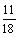 .
.
5、解:设A为取到两个蓝色球和一个黄色球的事件,B为先取到两个蓝色球,第三次取到红色球的事件,A、B互斥.
∴P(A+B)=P(A)+P(B)=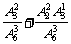 =
= ,即所求概率为
,即所求概率为
6、(1)从口袋中任取一个正方体,恰有两面涂有红色的概率是P= .
.
(2)从口袋中任取两个正方体,两个正方体表面都未涂有红色的概率为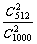 ,故其中至少有一个面上涂有红色的概率为P=1-
,故其中至少有一个面上涂有红色的概率为P=1-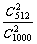 =0.738.
=0.738.
5、(Ⅰ)解法:三支弱队在同一组的概率为 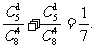
故有一组恰有两支弱队的概率为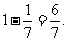
(Ⅱ)解法一:A组中至少有两支弱队的概率
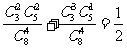
5解:(1)如果按指标的个数进行分类,讨论比较复杂,可构造模型,即用5个隔板插入10个指标中的9个空隙,即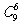 即为所求。
即为所求。
(2)先拿3个指标分别给二班1个,三班2个,则问题转化为7个优秀名额分给三个班,每班至少一个,同(1)知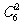 即为所求。
即为所求。
6、、[解析]:(1)在使用赋值法前,应先将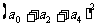
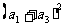 变形为:
变形为:
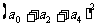 ―
―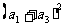 =
=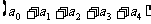
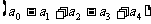
才能发现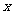 应取什么特殊值:
应取什么特殊值:
令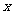 = ―1,则
= ―1,则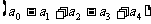 =
=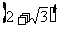
令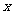 =1则
=1则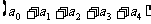 =
=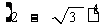
因此: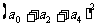 ―
―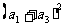 =
=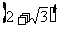 ·
·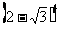 =
=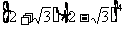 =1
=1
(2)因为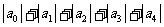 =
=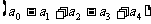 =
=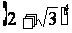 ,而
,而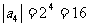 所以,
所以,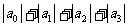 =
=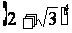 ―16
―16
6、从一批有5个合格品与3个次品的产品中,一件一件地抽取产品,设各个产品被抽到的可能性相同.记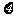 为直到取出的是合格品为止时所需抽取的次数,分别在下列三种情形下求出:(1) 每次抽取的产品都不放回到这批产品中的
为直到取出的是合格品为止时所需抽取的次数,分别在下列三种情形下求出:(1) 每次抽取的产品都不放回到这批产品中的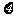 的分布列和所需平均抽取的次数;
的分布列和所需平均抽取的次数;
(2) 每次抽取的产品都立即放回到这批产品中,然后再抽取一件产品的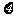 的分布列;
的分布列;
(3) 每次抽取一件产品后,总将一件合格品放入这批产品中的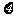 的分布列.
的分布列.
专题三答案:
5、蓝球运动员在比赛中每次罚球命中得1分,罚不中得0分,已知某运动员罚球命中的概率为0.7,则他罚球1次得分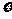 的期望、方差、标准差分别是多少?
的期望、方差、标准差分别是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com