
14.掌握函数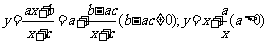 的图象和性质;
的图象和性质;
|
函数 |
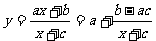 (b – ac≠0) (b – ac≠0) |
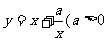 ) ) |
||||||||||||||||
|
定义域 |
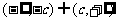 |
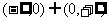 |
||||||||||||||||
|
值域 |
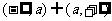 |
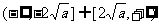 |
||||||||||||||||
|
奇偶性 |
非奇非偶函数 |
奇函数 |
||||||||||||||||
|
单调性 |
当b-ac>0时:分别在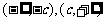 上单调递减; 上单调递减;当b-ac<0时:分别在 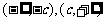 上单调递增; 上单调递增; |
在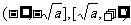 上单调递增; 上单调递增;在 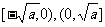 上单调递减; 上单调递减; |
||||||||||||||||
|
图象  |
 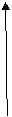 
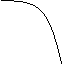  
|

|
13.依据单调性,利用一次函数在区间上的保号性可解决求一类参数的范围问题: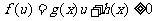 (或
(或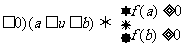 (或
(或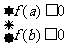 );
);
12.恒成立问题的处理方法:(1)分离参数法;(2)转化为一元二次方程的根的分布列不等式(组)求解;
11.处理二次函数的问题勿忘数形结合;二次函数在闭区间上必有最值,求最值问题用“两看法”:一看开口方向;二看对称轴与所给区间的相对位置关系;
10.对于反函数,应掌握以下一些结论:(1)定义域上的单调函数必有反函数;(2)奇函数的反函数也是奇函数;(3)定义域为非单元素集的偶函数不存在反函数;(4)周期函数不存在反函数;(5)互为反函数的两个函数具有相同的单调性;(5) y=f(x)与y=f-1(x)互为反函数,设f(x)的定义域为A,值域为B,则有f[f--1(x)]=x(x∈B),f--1[f(x)]=x(x∈A).
9.判断对应是否为映射时,抓住两点:(1)A中元素必须都有象且唯一;(2)B中元素不一定都有原象,并且A中不同元素在B中可以有相同的象;
8.能熟练地用定义证明函数的单调性,求反函数,判断函数的奇偶性。
7.(1)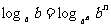 (a>0,a≠1,b>0,n∈R+); (2) l og a N=
(a>0,a≠1,b>0,n∈R+); (2) l og a N=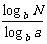 ( a>0,a≠1,b>0,b≠1);
( a>0,a≠1,b>0,b≠1);
(3) l og a b的符号由口诀“同正异负”记忆; (4) a log a N= N ( a>0,a≠1,N>0 );
6.a≥f(x)
恒成立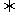 a≥[f(x)]max,; a≤f(x)
恒成立
a≥[f(x)]max,; a≤f(x)
恒成立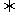 a≤[f(x)]min;
a≤[f(x)]min;
5.方程k=f(x)有解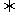 k∈D(D为f(x)的值域);
k∈D(D为f(x)的值域);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com