
5. (2008·大连质检)读右图,回答下列问题。
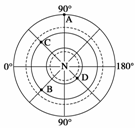
(2008·大连质检)读右图,回答下列问题。
(1)在图中标明地球自转的方向。
(2)A点位于B点的 方向,B点位于C点的 方向,D点位于
N点的 方向。
(3)在A、B、C、D四点中,位于东半球的有 ,位于西半球
的有 。
(4)若一架飞机从C地飞往D地,沿最近路线的飞行方向是 。
(5)若一架飞机从A地飞往B地,沿最近路线的飞行方向是 。
答案 (1)逆时针方向,图略。 (2)西南 正东 正南 ?(3)B、D A、C (4)先向正北方向飞行,到达北极点后沿经线向正南飞行 (5)先向东北,再向东南
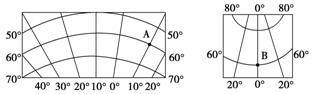
4.当B点的区时为6月22日4时时,全球以哪两条经线为界,分属两个日期 ( )
A.20°W和160°E B.120°E和180°
C.160°E和180° D.60°W和180°
答案 D
3.一架飞机6月22日从B点飞往A点,沿直线飞行,飞机朝哪个方向飞行 ( )
A.东北 B.西北 C.西南 D.东南
答案 D
2.一架飞机从M点出发,以1 100千米/小时的速度向北飞越北极点后继续沿经线圈飞行,
8小时后到达的地理位置是 ( )
A.100°W,40°N B.100°E,50°N
C.100°E,40°N D.100°W,50°N
答案 C
读下面两幅经纬网图,回答3-4题。
1.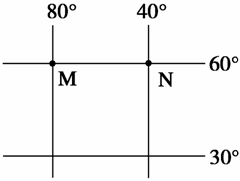 若某人从M点出发,依次向正东、正南、正西和正北方分别前进110千米,则其最终的位置
( )
若某人从M点出发,依次向正东、正南、正西和正北方分别前进110千米,则其最终的位置
( )
A.回到M点
B.在M点的正南方向
C.在M点的正东方向
D.在M点的正西方向
答案 C
3.[解]:(1)由于点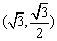 在椭圆上,
在椭圆上,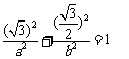 ------1分
------1分
2 =4,
------2分
=4,
------2分
椭圆C的方程为 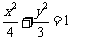 --------3分
--------3分
焦点坐标分别为(-1,0) ,(1,0)-----------4分
(2)设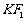 的中点为B(x, y)则点
的中点为B(x, y)则点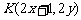 --------6分
--------6分
把K的坐标代入椭圆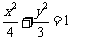 中得
中得 -----8分
-----8分
线段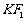 的中点B的轨迹方程为
的中点B的轨迹方程为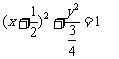 ----------10分
----------10分
(3)过原点的直线L与椭圆相交的两点M,N关于坐标原点对称
设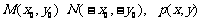 ----11分
----11分
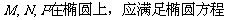 ,得
,得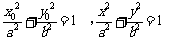 ------12分
------12分
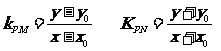 -------------------13分
-------------------13分
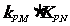 =
=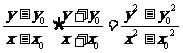 =
= -----------15分
-----------15分
故: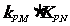 的值与点P的位置无关,同时与直线L无关,-----16分
的值与点P的位置无关,同时与直线L无关,-----16分
1 (2008学年度第一学期上海市普陀区高三年级质量调研第16题) (本题满分12分)设点 为椭圆
为椭圆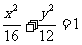 的左焦点,点
的左焦点,点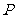 是椭圆上的动点.试求
是椭圆上的动点.试求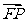 的模的最小值,并求此时点
的模的最小值,并求此时点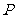 的坐标.
的坐标.
答案:解:由条件,可得 ,故左焦点
,故左焦点 的坐标为
的坐标为 .
.
设 为椭圆上的动点,由于椭圆方程为
为椭圆上的动点,由于椭圆方程为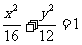 ,故
,故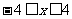 .
.
因为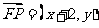 ,所以
,所以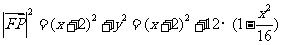
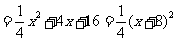 ,
,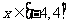
由二次函数性质可知,当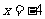 时,
时,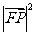 取得最小值4.
取得最小值4.
所以,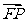 的模的最小值为2,此时点
的模的最小值为2,此时点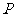 坐标为
坐标为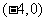 .
.
2 (2008学年度第一学期上海市普陀区高三年级质量调研第16题)(本题满分12分)设点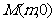 在椭圆
在椭圆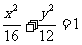 的长轴上,点
的长轴上,点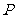 是椭圆上任意一点. 当
是椭圆上任意一点. 当 的模最小时,点
的模最小时,点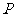 恰好落在椭圆的右顶点,求实数
恰好落在椭圆的右顶点,求实数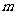 的取值范围.
的取值范围.
答案:解:设 为椭圆上的动点,由于椭圆方程为
为椭圆上的动点,由于椭圆方程为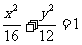 ,故
,故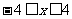 .
.
因为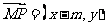 ,所以
,所以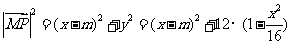
推出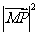
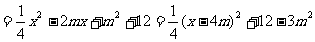 .
.
依题意可知,当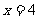 时,
时,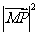 取得最小值.而
取得最小值.而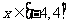 ,
,
故有 ,解得
,解得 .
.
又点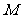 在椭圆的长轴上,即
在椭圆的长轴上,即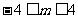 . 故实数
. 故实数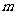 的取值范围是
的取值范围是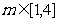 .
.
3 (上海市青浦区2008学年高三年级第一次质量调研第20题)(本题满分16分)第1小题满分4分,第2小题满分12分.
在平面直角坐标系 中,已知圆
中,已知圆 的圆心在第二象限,半径为
的圆心在第二象限,半径为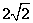 且与直线
且与直线 相切于原点
相切于原点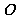 .椭圆
.椭圆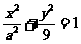 与圆
与圆 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为 .
.
(1)求圆 的方程;
的方程;
(2)圆 上是否存在点
上是否存在点 ,使
,使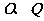 关于直线
关于直线 为圆心,
为圆心, 为椭圆右焦点)对称,若存在,请求出点
为椭圆右焦点)对称,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
答案:解:(1)由题意知:圆心(2,2),半径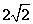 ,圆C:
,圆C:
(2)由条件可知 ,椭圆
,椭圆 ,
,
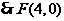
(解法1)若存在,直线CF的方程的方程为 即
即
设Q(x , y),则 ,
,
解得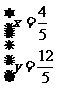 ,所以存在点Q,Q的坐标为
,所以存在点Q,Q的坐标为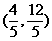 .
.
(解法2)由条件知OF=QF,设Q(x , y),则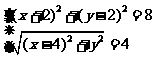 ,
,
解得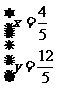 ,所以存在点Q,Q的坐标为
,所以存在点Q,Q的坐标为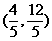 .
.
3.(08年上海市部分重点中学高三联考21)(4+6+6)设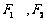 分别是椭圆C:
分别是椭圆C: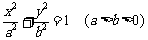 的左右焦点
的左右焦点
(1)设椭圆C上的点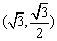 到
到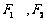 两点距离之和等于4,写出椭圆C的方程和焦点坐标
两点距离之和等于4,写出椭圆C的方程和焦点坐标
(2)设K是(1)中所得椭圆上的动点,求线段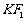 的中点B的轨迹方程
的中点B的轨迹方程
(3)设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为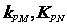 试探究
试探究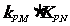 的值是否与点P及直线L有关,并证明你的结论。
的值是否与点P及直线L有关,并证明你的结论。
2.解:(1)焦点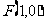 ,过抛物线的焦点且倾斜角为
,过抛物线的焦点且倾斜角为 的直线方程是
的直线方程是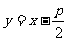
由
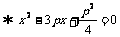
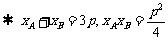

( 或 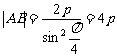 )
)
(2)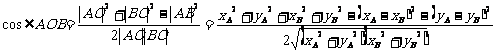

∴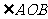 的大小是与
的大小是与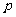 无关的定值,
无关的定值,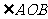
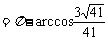 。
。
2.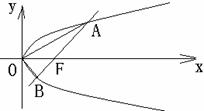 (上海市高考模拟试题19)过直角坐标平面
(上海市高考模拟试题19)过直角坐标平面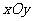 中的抛物线
中的抛物线 的焦点
的焦点 作一条倾斜角为
作一条倾斜角为 的直线与抛物线相交于A,B两点。
的直线与抛物线相交于A,B两点。
(1)用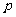 表示A,B之间的距离;
表示A,B之间的距离;
(2)证明: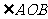 的大小是与
的大小是与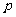 无关的定值,
无关的定值,
并求出这个值。
1.[解] 设所求轨道方程为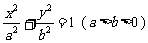 ,
, .
.
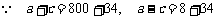 ,
,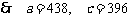 .
…… 4分
.
…… 4分
于是  .
.
 所求轨道方程为
所求轨道方程为 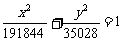 .
…… 6分
.
…… 6分
设变轨时,探测器位于 ,则
,则
 ,
, ,
,
解得 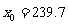 ,
,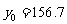 (由题意).
…… 10分
(由题意).
…… 10分
 探测器在变轨时与火星表面的距离为
探测器在变轨时与火星表面的距离为
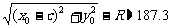 .
…… 13分
.
…… 13分
答:探测器在变轨时与火星表面的距离约为187百公里. …… 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com