
1、采用简单随机抽样时,常用的方法有____________、__________________.
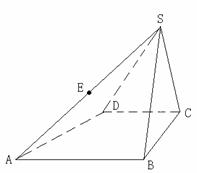
30.如图所示,四棱锥S-ABCD的底面是直角梯形,
∠ABC=∠BCD=90°,AB=BC=SB=SC=2CD=2,侧面SBC⊥底面ABCD.
(1)求四棱锥S-ABCD的体积;
(2)过SA的中点E作底面的垂线,试确定垂足H的位置.
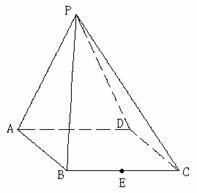
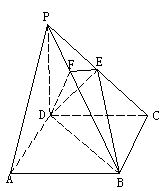
29.如图所示,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°的菱形,侧面PAD为正三角形,其所在平面垂直于底面ABCD.
(1)求证:AD⊥PB;
(2)若E为BC的中点,能否在棱PC上找到一点F,
使平面DEF⊥平面ABCD,并证明你的结论.
28. 如图所示,在侧棱垂直于底面的三棱柱ABC-A1B1C1中,
如图所示,在侧棱垂直于底面的三棱柱ABC-A1B1C1中,
AC=3,AB=5,cos∠CAB=3/5,AA1=4,点D是AB的中点.
(1)求证:AC⊥BC1 ;
(2)求证:AC1∥平面CDB1 ;
(3)求三棱锥A1-B1CD的体积.
27.如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD的中点.
 (1)求证:EN∥平面PDC;
(1)求证:EN∥平面PDC;
(2)求证:BC⊥平面PEB;
(3)求证:平面PBC⊥平面ADMN.
26.[2007年普通高等学校招生全国统一考试(安微卷)数学(文科)第17题](本小题满分14分)
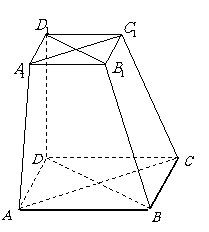 如图,在六面体
如图,在六面体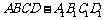 中,四边形
中,四边形 是边长为2的正方形,四边形
是边长为2的正方形,四边形 是边长为1的正方形,
是边长为1的正方形, 平面
平面 ,
, 平面
平面 ,
,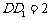 .
.
(Ⅰ)求证: 与
与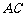 共面,
共面, 与
与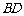 共面.
共面.
(Ⅱ)求证:平面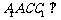 平面
平面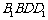 ;
;
(Ⅲ)略.
25.[2008年普通高等学校招生全国统一考试(四川)数学(文史类)第19题](本小题满分12分)
 如图,面ABEF⊥面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥
如图,面ABEF⊥面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥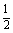 AD,BE∥
AD,BE∥ AF,G、H分别是FA、FD的中点。
AF,G、H分别是FA、FD的中点。
(Ⅰ)证明:四边形BCHG是平行四边形;
(Ⅱ)C、D、E、F四点是否共面?为什么?
(Ⅲ)设AB=BE,证明:平面ADE⊥平面CDE.
24.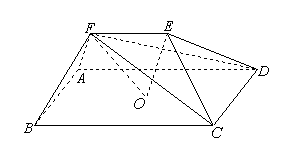 (2006年天津卷)如图,在五面体
(2006年天津卷)如图,在五面体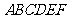 中,点
中,点 是矩形
是矩形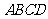 的对角线的交点,面
的对角线的交点,面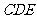 是等边三角形,棱
是等边三角形,棱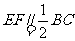 .
.
(1)证明 //平面
//平面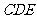 ;
;
(2)设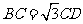 ,证明
,证明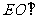 平面
平面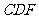 .
.
23. (2004年天津高考理工第19题,本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F。
(1)证明PA//平面EDB;
(2)证明PB⊥平面EFD;
(3)略。
22.[2008年普通高等学校招生全国统一考试文科数学第18题,理科数学第18题](本小题满分12分)
四棱锥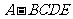 中,底面
中,底面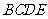 为矩形,侧面
为矩形,侧面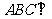 底面
底面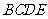 ,
,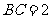 ,
, ,
,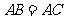 .
.
(Ⅰ)证明: ;
;
(Ⅱ)略(注:文理有差异).


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com