
1、掌握基数词、序数词构成
3、冠词常见的习惯搭配用法
2、不定冠词和定冠词的位置
1、不定冠词、定冠词和零冠词的基本用法
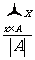 与
与 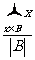
是互素的合数.(这里 与
与 分别表示有限数集
分别表示有限数集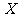 的所有元素之和及元素个数.)
的所有元素之和及元素个数.)
证 我们用 表示有限数集X中元素的算术平均.
表示有限数集X中元素的算术平均.
第一步,我们证明,正整数的n元集合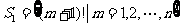 具有下述性质:对
具有下述性质:对 的任意两个不同的非空子集A,B,有
的任意两个不同的非空子集A,B,有 .
.
证明:对任意 ,
,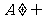 ,设正整数k满足
,设正整数k满足
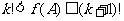 ,
①
,
①
并设l是使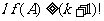 的最小正整数.我们首先证明必有
的最小正整数.我们首先证明必有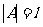 .
.
事实上,设 是A中最大的数,则由
是A中最大的数,则由 ,易知A中至多有
,易知A中至多有 个元素,即
个元素,即 ,故
,故 .又由
.又由 的定义知
的定义知

 ,故由①知
,故由①知 .特别地有
.特别地有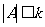 .
.
此外,显然 ,故由l的定义可知
,故由l的定义可知 .于是我们有
.于是我们有
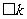 .
.
若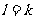 ,则
,则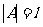 ;否则有
;否则有 ,则
,则
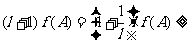
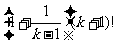
 .
.
由于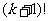 是A中最大元,故上式表明
是A中最大元,故上式表明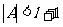 .结合
.结合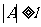 即知
即知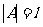 .
.
现在,若有 的两个不同的非空子集A,B,使得
的两个不同的非空子集A,B,使得 ,则由上述证明知
,则由上述证明知 ,故
,故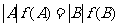 ,但这等式两边分别是A,B的元素和,利用
,但这等式两边分别是A,B的元素和,利用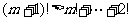 易知必须A=B,矛盾.
易知必须A=B,矛盾.
第二步,设K是一个固定的正整数,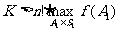 ,我们证明,对任何正整数x,正整数的n元集合
,我们证明,对任何正整数x,正整数的n元集合 具有下述性质:对
具有下述性质:对 的任意两个不同的非空子集A,B,数
的任意两个不同的非空子集A,B,数 与
与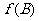 是两个互素的整数.
是两个互素的整数.
事实上,由 的定义易知,有
的定义易知,有 的两个子集
的两个子集 ,满足
,满足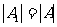 ,
,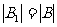 ,且
,且
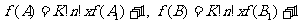 .
②
.
②
显然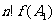 及
及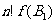 都是整数,故由上式知
都是整数,故由上式知 与
与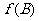 都是正整数.
都是正整数.
现在设正整数d是 与
与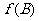 的一个公约数,则
的一个公约数,则 是d的倍数,故由②可知
是d的倍数,故由②可知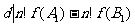 ,但由K的选取及
,但由K的选取及 的构作可知,
的构作可知, 是小于K的非零整数,故它是
是小于K的非零整数,故它是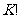 的约数,从而
的约数,从而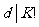 .再结合
.再结合 及②可知d=1,故
及②可知d=1,故 与
与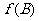 互素.
互素.
第三步,我们证明,可选择正整数x,使得 中的数都是合数.由于素数有无穷多个,故可选择n个互不相同且均大于K的素数
中的数都是合数.由于素数有无穷多个,故可选择n个互不相同且均大于K的素数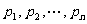 .将
.将 中元素记为
中元素记为 ,则
,则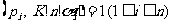 ,且
,且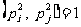 (对
(对 ),故由中国剩余定理可知,同余方程组
),故由中国剩余定理可知,同余方程组
 ,
,
有正整数解.
任取这样一个解x,则相应的集合 中每一项显然都是合数.结合第二步的结果,这一n元集合满足问题的全部要求.
中每一项显然都是合数.结合第二步的结果,这一n元集合满足问题的全部要求.
解 当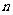
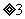 为奇数时,存在合乎要求的染法;当
为奇数时,存在合乎要求的染法;当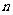
 为偶数时,不存在所述的染法。
为偶数时,不存在所述的染法。
每3个顶点形成一个三角形,三角形的个数为 个,而颜色的三三搭配也刚好有
个,而颜色的三三搭配也刚好有 种,所以本题相当于要求不同的三角形对应于不同的颜色组合,即形成一一对应.
种,所以本题相当于要求不同的三角形对应于不同的颜色组合,即形成一一对应.
我们将多边形的边与对角线都称为线段.对于每一种颜色,其余的颜色形成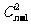 种搭配,所以每种颜色的线段(边或对角线)都应出现在
种搭配,所以每种颜色的线段(边或对角线)都应出现在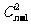 个三角形中,这表明在合乎要求的染法中,各种颜色的线段条数相等.所以每种颜色的线段都应当有
个三角形中,这表明在合乎要求的染法中,各种颜色的线段条数相等.所以每种颜色的线段都应当有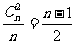 条.
条.
当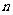 为偶数时,
为偶数时, 不是整数,所以不可能存在合乎条件的染法.下设
不是整数,所以不可能存在合乎条件的染法.下设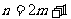 为奇数,我们来给出一种染法,并证明它满足题中条件.自某个顶点开始,按顺时针方向将凸
为奇数,我们来给出一种染法,并证明它满足题中条件.自某个顶点开始,按顺时针方向将凸 边形的各个顶点依次记为
边形的各个顶点依次记为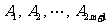 .对于
.对于 ,按
,按 理解顶点
理解顶点 .再将
.再将 种颜色分别记为颜色
种颜色分别记为颜色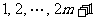 .
.
将边 染为颜色
染为颜色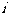 ,其中
,其中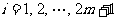 .再对每个
.再对每个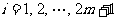 ,都将线段(对角线)
,都将线段(对角线) 染为颜色
染为颜色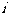 ,其中
,其中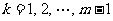 .于是每种颜色的线段都刚好有
.于是每种颜色的线段都刚好有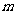 条.注意,在我们的染色方法之下,线段
条.注意,在我们的染色方法之下,线段 与
与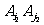 同色,当且仅当
同色,当且仅当
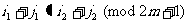 . ①
. ①
因此,对任何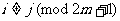 ,任何
,任何 ,线段
,线段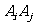 都不与
都不与 同色.换言之,如果
同色.换言之,如果
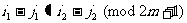 .
②
.
②
则线段 都不与
都不与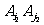 同色.
同色.
任取两个三角形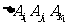 和
和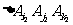 ,如果它们之间至多只有一条边同色,当然它们不对应相同的颜色组合.如果它们之间有两条边分别同色,我们来证明第3条边必不同颜色.为确定起见,不妨设
,如果它们之间至多只有一条边同色,当然它们不对应相同的颜色组合.如果它们之间有两条边分别同色,我们来证明第3条边必不同颜色.为确定起见,不妨设 与
与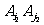 同色.
同色.
情形1:如果 与
与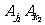 也同色,则由①知
也同色,则由①知
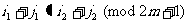 ,
,
 ,
,
将二式相减,得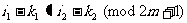 ,故由②知
,故由②知 不与
不与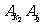 同色.
同色.
情形2:如果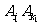 与
与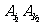 也同色,则亦由①知
也同色,则亦由①知
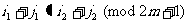 ,
,
 ,
,
将二式相减,亦得 ,亦由②知
,亦由②知 与
与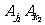 不同色.总之,
不同色.总之,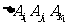 与
与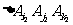 对应不同的颜色组合.
对应不同的颜色组合.
解 不妨设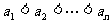 ,则对
,则对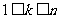 ,有
,有
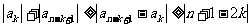 ,
,
所以 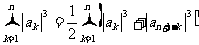

 .
.
当n为奇数时, 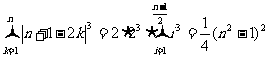 .
.
当n为偶数时, 
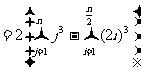
 .
.
所以,当n为奇数时, ,当n为偶数时,
,当n为偶数时, ,等号均在
,等号均在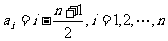 时成立.
时成立.
因此, 的最小值为
的最小值为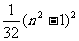 (n为奇数),或者
(n为奇数),或者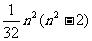 (n为偶数).
(n为偶数).
解 先证一个引理:顶点在P中的凸m边形至多有两个锐角,且有两个锐角时,这两个锐角必相邻.
事实上,设这个凸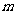 边形为
边形为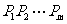 ,只考虑至少有一个锐角的情况,此时不妨设
,只考虑至少有一个锐角的情况,此时不妨设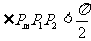 ,则
,则
 ,
,
更有 .
.
而 +
+

 ,故其中至多一个为锐角,这就证明了引理.
,故其中至多一个为锐角,这就证明了引理.
由引理知,若凸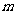 边形中恰有两个内角是锐角,则它们对应的顶点相邻.
边形中恰有两个内角是锐角,则它们对应的顶点相邻.
在凸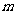 边形中,设顶点
边形中,设顶点 与
与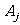 为两个相邻顶点,且在这两个顶点处的内角均为锐角.设
为两个相邻顶点,且在这两个顶点处的内角均为锐角.设 与
与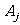 的劣弧上包含了
的劣弧上包含了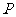 的
的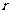 条边(
条边(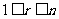 ),这样的
),这样的 在
在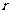 固定时恰有
固定时恰有 对.
对.
(1) 若凸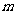 边形的其余
边形的其余 个顶点全在劣弧
个顶点全在劣弧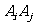 上,而
上,而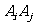 劣弧上有
劣弧上有 个
个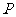 中的点,此时这
中的点,此时这 个顶点的取法数为
个顶点的取法数为 .
.
(2) 若凸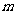 边形的其余
边形的其余 个顶点全在优弧
个顶点全在优弧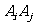 上,取
上,取 ,
,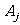 的对径点
的对径点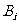 ,
,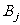 ,由于凸
,由于凸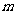 边形在顶点
边形在顶点 ,
,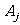 处的内角为锐角,所以,其余的
处的内角为锐角,所以,其余的 个顶点全在劣弧
个顶点全在劣弧 上,而劣弧
上,而劣弧 上恰有
上恰有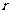 个
个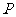 中的点,此时这
中的点,此时这 个顶点的取法数为
个顶点的取法数为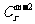 .
.
所以,满足题设的凸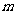 边形的个数为
边形的个数为

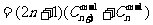 .
.
解:若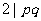 ,不妨设
,不妨设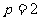 ,则
,则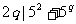 ,故
,故 .
.
由Fermat小定理,  ,得
,得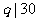 ,即
,即 .易验证素数对
.易验证素数对 不合要求,
不合要求,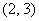 ,
, 合乎要求.
合乎要求.
若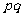 为奇数且
为奇数且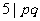 ,不妨设
,不妨设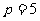 ,则
,则 ,故
,故 .
.
当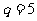 时素数对
时素数对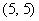 合乎要求,当
合乎要求,当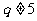 时,由Fermat小定理有
时,由Fermat小定理有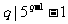 ,故
,故 .由于
.由于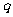 为奇素数,而626的奇素因子只有313,所以
为奇素数,而626的奇素因子只有313,所以 .经检验素数对
.经检验素数对 合乎要求.
合乎要求.
若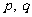 都不等于2和5,则有
都不等于2和5,则有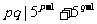 ,故
,故
 .
①
.
①
由Fermat小定理,得  ,
②
,
②
故由①,②得
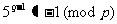 .
③
.
③
设 ,
,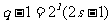 , 其中
, 其中 为正整数.
为正整数.
若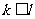 ,则由②,③易知
,则由②,③易知
 ,
,
这与 矛盾!所以
矛盾!所以 .
.
同理有 ,矛盾!即此时不存在合乎要求的
,矛盾!即此时不存在合乎要求的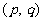 .
.
综上所述,所有满足题目要求的素数对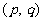 为
为
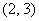 ,
,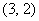 ,
, ,
,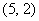 ,
,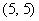 ,
, 及
及 .
.
(1)若A,B,C,D四点共圆,求证: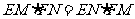 ;
;
(2)若 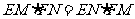 ,是否一定有A,B,C,D四点共圆?证明你的结论.
,是否一定有A,B,C,D四点共圆?证明你的结论.
 解(1)设Q,R分别是OB,OC的中点,连接EQ,MQ,FR,MR,则
解(1)设Q,R分别是OB,OC的中点,连接EQ,MQ,FR,MR,则
 ,
,
又OQMR是平行四边形,所以
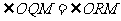 ,
,
由题设A,B,C,D四点共圆,所以
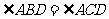 ,
,
于是 图1
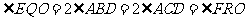 ,
,
所以
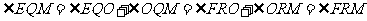 ,
,
故
 ,
,
所以 EM=FM,
同理可得 EN=FN,
所以
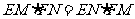 .
.
(2)答案是否定的.
当AD∥BC时,由于 ,所以A,B,C,D四点不共圆,但此时仍然有
,所以A,B,C,D四点不共圆,但此时仍然有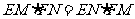 ,证明如下:
,证明如下:
如图2所示,设S,Q分别是OA,OB的中点,连接ES,EQ,MQ,NS,则
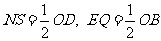 ,
,
所以
 .
①
.
①
又 ,所以
,所以
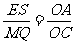 .
②
.
②
而AD∥BC,所以
 ,
③
,
③
由①,②,③得
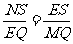 .
.
因为 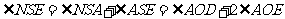 ,
,

 ,
,
即
 ,
,
所以
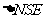 -
- ,
,
 故
故
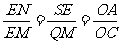 (由②).
(由②).
同理可得,
 ,
,
所以
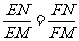 ,
,
从而
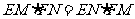 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com