
2.(05全国卷Ⅰ)设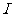 为全集,
为全集,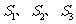 是
是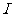 的三个非空子集,且
的三个非空子集,且 ,则下面论断正确的是(C)
,则下面论断正确的是(C)
(A)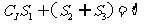 (B)
(B)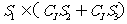
(C) (D)
(D)
1.(04年全国Ⅰ理)设A、B、I均为非空集合,且满足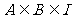 ,则下列各式中错误的是
( )
,则下列各式中错误的是
( )
(A)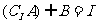 (B)
(B) 
(C) 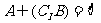 (D)
(D) 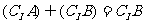
6. 有限集的元素个数
定义:有限集A的元素的个数叫做集合A的基数,记为card( A)规定 card(φ) =0.
基本公式:

(3) card(ðUA)= card(U)- card(A)
(4)设有限集合A, card(A)=n,则
(ⅰ)A的子集个数为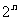 ; (ⅱ)A的真子集个数为
; (ⅱ)A的真子集个数为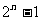 ;
;
(ⅲ)A的非空子集个数为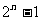 ;(ⅳ)A的非空真子集个数为
;(ⅳ)A的非空真子集个数为 .
.
(5)设有限集合A、B、C, card(A)=n,card(B)=m,m<n,则
(ⅰ) 若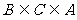 ,则C的个数为
,则C的个数为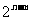 ;
;
(ⅱ) 若 ,则C的个数为
,则C的个数为 ;
;
(ⅲ) 若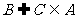 ,则C的个数为
,则C的个数为 ;
;
(ⅳ) 若 ,则C的个数为
,则C的个数为 .
.
5. 主要性质和运算律
(1)
包含关系: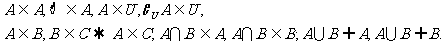
(2)
等价关系:
(3) 集合的运算律:
交换律: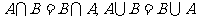
结合律: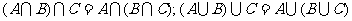
分配律:.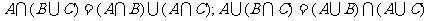
0-1律: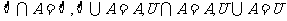
等幂律: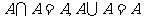
求补律:A∩ðUA=φ A∪ðUA=U ðUU=φ ðUφ=U ðU(ðUA)=A
反演律:ðU(A∩B)= (ðUA)∪(ðUB) ðU(A∪B)= (ðUA)∩(ðUB)
4. 集合运算:交、并、补.
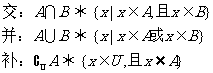
3. 集合元素的特征:确定性、互异性、无序性.
2. 集合的表示法:列举法、描述法、图形表示法.
1. 基本概念:集合、元素;有限集、无限集;空集、全集;符号的使用.
(2)掌握简单不等式的解法. (3)理解逻辑联结词"或"、"且"、"非"的含义.理解四种命题及其相互关系.掌握充分条件、必要条件及充要条件的意义.
集合的概念和运算(1)
(2)不等式的解法.含绝对值的不等式.
(3)逻辑联结词.四种命题.充分条件和必要条件.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com