5、四种命题的形式：

原命题：若P则q；　 逆命题：若q则p；

否命题：若┑P则┑q；逆否命题：若┑q则┑p。

(1)交换原命题的条件和结论，所得的命题是逆命题；

　(2)同时否定原命题的条件和结论，所得的命题是否命题；

　(3)交换原命题的条件和结论，并且同时否定，所得的命题是逆否命题．

4、常用正面词语的否定如下表：

3、“或”、　 “且”、　 “非”的真值判断

(1)“非p”形式复合命题的真假与P的真假相反；

(2)“p且q”形式复合命题当P与q同为真时为真，其他情况时为假；

(3)“p或q”形式复合命题当p与q同为假时为假，其他情况时为真．

2、逻辑联结词、简单命题与复合命题：

“或”、“且”、“非”这些词叫做逻辑联结词；不含有逻辑联结词的命题是简单命题；由简单命题和逻辑联结词“或”、“且”、“非”构成的命题是复合命题。

构成复合命题的形式：p或q(记作“p∨q” )；p且q(记作“p∧q” )；非p(记作“┑q” ) 。

1、命题的定义：可以判断真假的语句叫做命题。

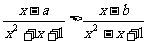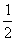3、如果不等式的解集为(，1)，则=　　　　　 .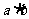

2、不等式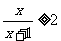的解集为　　　　　　　　　　 .

1、不等式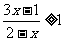的解集为……………………………(　　 )

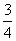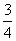(A){x|≤x≤2}　　　　　　　　　　　　　 (B) {x|≤x<2}　　

(C) {x|x>2或者x≤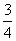} 　　　　　　　　　　(D){x|x＜2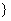

例1.解不等式：(x－1)·(x－2)·(x－3)·(x－4)>120

例2. 解不等式：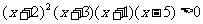

例3. 解不等式：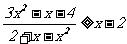

例4．解不等式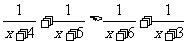

例5. 若不等式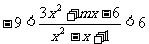对一切x恒成立,求实数m的范围

例6.求适合不等式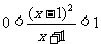的整数x的值.

例7. 解关于x的不等式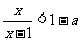

4、不等式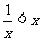的解集为　　　　　　　　　　 .