3.　　　 图象变换与变量替换的关系

　　　 (1)平移变换

　 　　(2)对称变换：， ，， ， 　， ，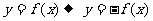

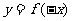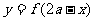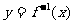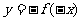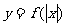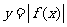
　 　　(3)伸缩变换： ，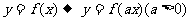

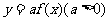
2.　　　 正比例函数、反比例函数、二次函数的图象及几种基本初等函数的图象.

数形结合是中学数学的重要的数学思想方法，尤其是函数的图象更是历年高考的热点.函数图象是函数的一种表达形式，形象的显示了函数的性质，为研究数量关系提供了“形”的直观性，它是探求解题途径，获得问题的结果的重要工具.

1.　　　 用描点法作函数的图象.

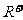15、设是定义在上的增函数，并且对任意的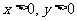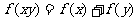，总成立。

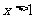　(1)求证：时，；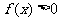

　(2)如果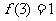，解不等式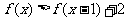

14、已知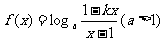是奇函数。

　 (1)求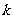的值，并求该函数的定义域；

　 (2)根据(1)的结果，判断在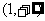上的单调性，并给出证明。

13、已知奇函数是定义在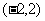上的减函数，若，求实数的取值范围。

12、已知函数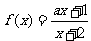在区间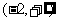上是增函数，试求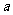的取值范围。

11、已知是R上的增函数，A(0，－1)，B(3,1)是其图象上的两点，则不等式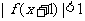 的解集为__________

10、已知偶函数在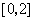内单调递减，若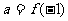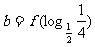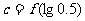，，，则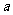、、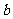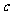之间的大小关系是_____________

9、(04年上海卷.文理10)若函数f(x)=a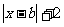在[0,+∞]上为增函数,则实数a、b的取值范围是　　 　　　　　　.