
例1、(1)一种产品的年产量原来是a件,在今后的m年内,计划使年产量平均每年比上一年增加p%,写出年产量随经过年数变化的函数关系式。
(2)一种产品的成本原来是a件,在今后的m年内,计划使成本平均每年比上一年降低p%,写出成本随经过年数变化的函数关系式。
|
级数 |
全月纳税所得额 |
税率 |
|
1 |
不超过500元的部分 |
5% |
|
2 |
超过500元至2000元的部分 |
10% |
|
3 |
超过2000至5000元的部分 |
15% |
|
… |
… |
… |
|
9 |
超过10000元的部分 |
45% |
例2、“依法纳税是每个公民应尽的义务。”国家征收个人所得税是分段计算的,月收入不超过800元,免征收个人所得税,超过800元的部分需征税,设全月应纳税所得额为,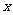 =全月收入-800,税率见右表:
=全月收入-800,税率见右表:
①若应纳税额为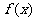 ,试用分段函数表示1~3级纳税额
,试用分段函数表示1~3级纳税额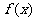 的计算公式;
的计算公式;
②某人2003年1月份总收入为3000元,试计算该人此月份应缴纳个人所得税多少元?
③某人1月份应缴纳此项税款26.78元,则他当月工资总收入介于: ( )
(A)800~900元 (B)900~1200元 (C)1200~1500元 (D)1500~2800元
例3、某地区上年度电价为0.8元/kw h,年用电量为a kw h,本年度计划将电价降到0.55元/kw h至0.75元/kw h之间,而用户期望电价为0.4元/kw h。经测算,下调电价后新增的用电量与实际电价和用户期望电价的差成反比(比例系数为k),该地区电力的成本价为0.3元/kw h
(1) 写出本年度电价下调后,电力部门的收益y与实际电价x的函数关系式;
(2) 设k=0.2a,当电价最低定为多少时仍保证比电力部门的收益比上年至少增长20%(注:收益=实际用电量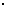 (实际电价-成本价))
(实际电价-成本价))
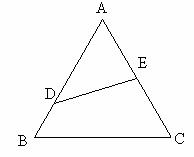 例4、如图所示,某校把一块边长为2a的等边
例4、如图所示,某校把一块边长为2a的等边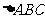 的边角地辟为生物园,图中DE把生物园分成面积相等的两部分,D在AB上,E在AC上。
的边角地辟为生物园,图中DE把生物园分成面积相等的两部分,D在AB上,E在AC上。
(1)
设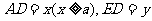 ,求用x表示y的函数关系式;
,求用x表示y的函数关系式;
(2) 如果DE是灌溉水管的位置,为了省钱,希望它最短,DE的位置应该在哪里?如果DE是参观线路,即希望它最长,DE的位置又应该在哪里?
4、用一张钢板制作一个容积为4m3的无盖长方体水箱,可用的长方形钢板有四种不同的规格(长 宽的尺寸如各选项所示;单位为m)若既要够用,又要所剩最少,则应选钢板的规格是:
(
)
宽的尺寸如各选项所示;单位为m)若既要够用,又要所剩最少,则应选钢板的规格是:
(
)
(A) (B)
(B)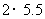 (C)
(C) (D)
(D)
基本训练:1、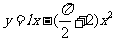 ;
; ;
; 2、D 3、D 4、C
2、D 3、D 4、C
例题:1(1)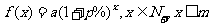 (2)
(2)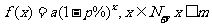 2(1)
2(1)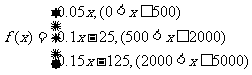 (2)205元 (3)C 3(1)
(2)205元 (3)C 3(1)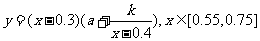 (2)0.6元/kwh 4(1)
(2)0.6元/kwh 4(1)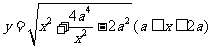 (2)当
(2)当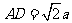 且DE∥BC时DE最短;当D为AB中点,E与C重合或D与B重合,E为AC中点时,DE最长。
且DE∥BC时DE最短;当D为AB中点,E与C重合或D与B重合,E为AC中点时,DE最长。
3、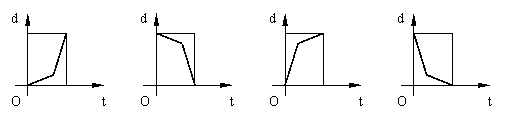 某学生离家去学校,为了锻炼身体,一开始跑步前进,跑累了再走余下的路程,下图中,纵轴表示离学校的距离,横轴表示出发后的时间,则下列四个图形中较符合该学生的走法是:
( )
某学生离家去学校,为了锻炼身体,一开始跑步前进,跑累了再走余下的路程,下图中,纵轴表示离学校的距离,横轴表示出发后的时间,则下列四个图形中较符合该学生的走法是:
( )
(A) (B) (C) (D)
2、某一种商品降价10% 后,欲恢复原价,则应( )
后,欲恢复原价,则应( )
(A)10% (B)9% (C)11%
(D)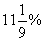
1、用长为L的铁丝弯成下部为长方形,上部为半圆形的框架(如图)。若正方形边长为2x,则此框架的面积y与x的函数关系式:____________,定义域______________,值域________________
2、与函数有关的应用题,经常涉及物价、路程、产值、环保等实际问题,也可涉及角度、面积、体积、造价的最优化问题。解答这类问题的关键是确切建立相应的函数解析式,然后应用函数、方程和不等式的有关知识加以综合解答。
1、解答数学应用题的关键有两点:
一是认真读题,缜密审题,确切理解题意,明确问题的实际背景,然后进行科学的抽象概括,将实际问题归纳为相应的数学问题;
二是要合理的选取参变数,设定变元后就要寻找它们之间的内在联系,选用恰当的代数式表示问题中的关系,处理相应的函数、方程、不等式等数学模型;最终求解数学模型使实际问题得到解决。
一般的解题程序是:


 读题
建模
求解
反馈
读题
建模
求解
反馈
(文字语言) (数学语言) (数学应用) (检验作答)
15、设集合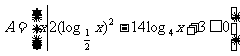 ,若函数
,若函数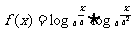 ,其中
,其中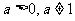 ,当
,当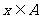 时,其值域为
时,其值域为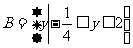 ,求实数
,求实数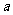 的值。
的值。
14、设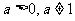 ,如果函数
,如果函数 在
在 上的最大值为
上的最大值为 ,求
,求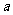 的值。
的值。
13、已知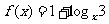 ,
,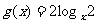 ,试比较
,试比较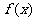 与
与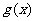 的大小关系。
的大小关系。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com