
2、函数与其它代数知识,主要是方程、不等式、数列的综合问题;
函数思想是高中数学的主线,函数知识贯穿高中代数始终,函数知识是高中数学最重要的内容。函数综合问题主要表现在以下几个方面:
1、函数的概念、性质和方法的综合问题;
8、某工厂拟建一座平面图(如图所示)为矩形且面积为200平方米的三级污水处理池,由于地形限制,长、宽都不能超过16米,如果池外周壁建造单价为每米400元,中间池壁造价为每米248元,池底建造单价为每平方米80元。(池壁的厚度忽略不计,且池无盖)
(1) 写出总造价 (元)与污水处理池长
(元)与污水处理池长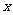 (米)的函数关系式,并指出定义域。
(米)的函数关系式,并指出定义域。
(2) 求污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求出最低总造价?

7、某租赁公司拥有汽车100辆,当每辆汽车的月租金为3000元时,可全部租出。当每辆车的月租金每增加50元时,未租出的车辆会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1) 当每辆车的月租金定为3600元时,能租出多少辆车?
(2) 当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
6、在国内投寄平信,每封信不超过20克重付邮资80分,超过20克重而不超过40克重付邮资160分,将每封信的应付邮资(分)表示为信重x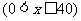 克的函数,其表达式为
克的函数,其表达式为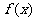 =________________,并画出整个函数的图象.
=________________,并画出整个函数的图象.
5、据新华社2002年3月12日电,1985年到2000年间,我国农村人均居住面积如图1所示,其中从_________年到___________年的五年间增长最快。
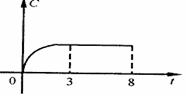

图1 图2
4、某工厂八年来某种产品总产量c与时间t(年)的函数如图2所示,下列四种说法:
(1)前三年中产量增长的速度越来越快;(2)前三年中产量增长的速度越来越慢;(3)第三年后,这种产品停止生产;(4)第三年后,年产量保持不变,其中说法正确的序号是_________________.
3、某汽车运输公司,购买了一批豪华大客车投入客运,据市场分析,每辆客车营运的总利润 万元与营运年数
万元与营运年数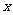
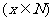 的关系为
的关系为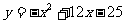 ,则每辆客车营运多少年使其营运年平均利润最大.
( )
,则每辆客车营运多少年使其营运年平均利润最大.
( )
(A) 2 (B) 4 (C) 5 (D) 6
2、今有一组实验数据如右:现准备用下列函数中的一个近似的表示这些数据满足的规律,其中最接近的一个是: ( )
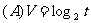
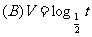
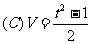
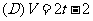
1、拟定从甲地到乙地通话m分钟的电话费由f(m)=1.06(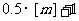 )给她出,其中m>0,[m]是大于或等于的最小整数。如[4]=4、[2.7]=3,[3.8]=4,则从甲地到乙地通话时间5.5分钟的电话费为 ( )
)给她出,其中m>0,[m]是大于或等于的最小整数。如[4]=4、[2.7]=3,[3.8]=4,则从甲地到乙地通话时间5.5分钟的电话费为 ( )
(A)3.71 (B)3.97 (C)4.24 (D)4.77
|
t |
1.99 |
3.0 |
4.0 |
5.1 |
6.12 |
|
v |
1.5 |
4.04 |
7.5 |
12 |
18.01 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com