
6、(04年北京卷.文理14)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。
已知数列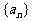 是等和数列,且
是等和数列,且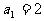 ,公和为5,那么
,公和为5,那么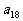 的值为______________,这个数列的前n项和
的值为______________,这个数列的前n项和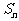 的计算公式为________________
的计算公式为________________
5、在数列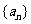 中,
中,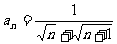 ,且Sn=9,则n=_____________.
,且Sn=9,则n=_____________.
4、已知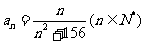 ,则在数列
,则在数列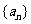 的最大项为____________.
的最大项为____________.
3、 已知数列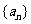 的通项公式为
的通项公式为 ,那么
,那么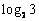 是这个数列的
是这个数列的
A.第3项 B.第4项 C.第5项 D.第6项
2、数列4,-1,,- ,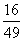 ,…的一个通项公式是
,…的一个通项公式是
A、 B、
B、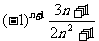 C、
C、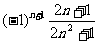 D、
D、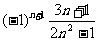
1、在数列1,1,2,3,5,8,13,x,34,55,…中,x的值是
A、19 B、 20 C、 21 D 、22
3. 求数列通项公式的一个重要方法:
对于任一数列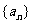 ,其通项
,其通项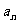 和它的前n项和
和它的前n项和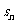 之间的关系是
之间的关系是

2. 数列的通项公式.
1. 数列的定义(一般定义,数列与函数)、数列的表示法.
(二)极限
(1)理解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题. (2)了解数列极限和函数极限的概念. (3)掌握极限的四则运算法则.会求某些数列与函数的极限. (4)了解函数连续的意义,理解闭区间上连续函数有最大值和最小值的性质. (三)导数
(1)了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等);掌握函数在一点处的导数的定义和导数的几何意义;理解导函数的概念. (2)熟记基本导数公式(c,xm(m为有理数),sinx,cosx,ex,ax,ln x,logax的导数);掌握两个函数和、差、积、商的求导法则.了解复合函数的求导法则,会求某些简单函数的导数. (3)理解可导函数的单调性与其导数的关系;了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两则异号);会求一些实际问题(一般指单峰函数)的最大值和最小值.
g3.1021数列的概念
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com