
3、数列极限的运算法则
如果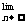 an=A,
an=A,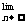 bn=B,那么(1)
bn=B,那么(1)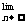 (an±bn)=A±B (2)
(an±bn)=A±B (2)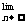 (an·bn)=A·B (3)
(an·bn)=A·B (3)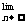
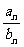 =
=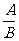 (B≠0)
(B≠0)
极限不存在的情况是1、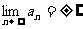 ;2、极限值不唯一,跳跃,如1,-1,1,-1….
;2、极限值不唯一,跳跃,如1,-1,1,-1….
注意:数列极限运算法则运用的前提:
(1)参与运算的各个数列均有极限;
(2)运用法则,只适用于有限个数列参与运算,当无限个数列参与运算时不能首先套用.
2、几个常用极限
①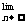 C=C(常数列的极限就是这个常数)
C=C(常数列的极限就是这个常数)
②设a>0,则特别地 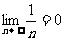
③设q∈(-1,1),则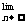 qn=0;
qn=0;
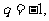 或
或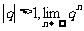 不存在。
不存在。
若无穷等比数列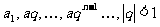 叫无穷递缩等比数列,其所有项的和(各项的和)为:
叫无穷递缩等比数列,其所有项的和(各项的和)为: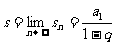
1、 数列极限定义
(1)定义:设{an}是一个无穷数列,a是一个常数,如果对于预先给定的任意小的正数ε,总存在正整数N,使得只要正整数n>N,就有|an-a|<ε,那么就称数列{an}以a为极限,记作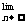 an=a。
an=a。
对前任何有限项情况无关。
*(2)几何解释:设ε>0,我们把区间(a-ε,a+ε)叫做数轴上点a的ε邻域;极限定义中的不等式|an-a|<ε也可以写成a-ε<an<a+ε,即an∈(a-ε,a+ε);因此,借助数轴可以直观地理解数列极限定义:不论a点的ε邻域怎么小,数列{an}从某一项以后的所有项都要进入这个邻域中,也可以说点a的任意小的ε邻域(a-ε,a+ε)中含有无穷数列{an}的几乎所有的项,而在这个邻域之外至多存在有限个项,由此可以想像无穷数列{an}的项是多么稠密地分布在点a的附近。
11.已知An=(1+lgx)n,Bn=1+nlgx+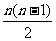 lg2x,其中n∈N,n³3,
lg2x,其中n∈N,n³3,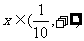 ,试比较
,试比较
AN与Bn的大小.
10. 
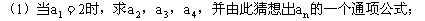

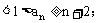

9. 求证: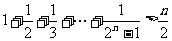 (
(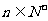 )
)
8.是否存在常数a,b,c,使得等式1·22+2·32+……+n(n+1)2=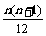 (an2+bn+c)对一切自然数n成立?并证明你的结论.
(an2+bn+c)对一切自然数n成立?并证明你的结论.
7.用数学归纳法证明(n+1)(n+2)…(n+n)=2n´1´2´3´…(2n─1)(n∈N),从“k到k+1”左端应增乘的代数式为 .
6.由归纳原理分别探求:
(1)凸n边形的内角和f(n)= ;
(2)凸n边形的对角线条数f(n)= ;
(3)平面内n个圆,其中每两个圆都相交于两点,且任意三个圆不相交于同一点,则该n个圆分平面区域数f(n)= .为真,进而需验证n= ,命题为真。
5. 则Sk+1
=
则Sk+1
=
(A) Sk + 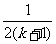 (B) Sk +
(B) Sk + 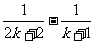
(C) Sk + 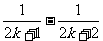 (D) Sk +
(D) Sk + 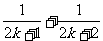
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com