
3、本节复习内容是数列极限在代数,平面几何、三角、解析几何中的综合应用,尤其要注意公式S=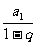 的运用。
的运用。
2、极限运算最终转化为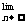 qn=0(|q|<1),
qn=0(|q|<1),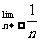 =0,
=0,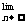 C=C(C为常数)
C=C(C为常数)
1、极限的四则运算,要特别注意四则运算的条件是否满足。
例1求下列极限
(1)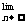 (
(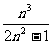 -
-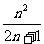 ) (2)
) (2)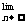 [
[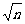 (
(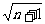 -
-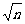 )]
)]
(3)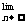 (
(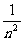 +
+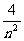 +
+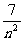 +…+
+…+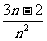 ) (4)
) (4)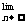
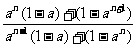 (a≠1)
(a≠1)
例2:已知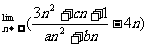 =5,求常数a、b、c的值。
=5,求常数a、b、c的值。
例3.设数列a1,a2,…,an,…的前n项的和Sn和an的关系是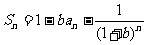 ,其中b是与n无关的常数,且b≠―1
,其中b是与n无关的常数,且b≠―1
(1)求an和an-1的关系式; (2)写出用n和b表示an的表达式;(3)当0<b<1时,求极限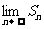
例4、已知数例{an}前n项之和Sn=1+kan(k为不是0、1的常数)。
(1)用n,k表示an; (2)若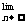 Sn=1,求k的取值范围。
Sn=1,求k的取值范围。
例5、某城市2001年末汽车保有量为30万辆,预计此后每年报废上一年末汽车保有量的6%,并且每年新增汽车数量相同,为保护城市环境,要求该城市汽车保有量不超过60万辆,那么每年新增汽车数量不应超过多少辆?
备用:某县地处水乡,县政府原计划从今年起填湖围造一部分生产和生活用地。但根据前几年抗洪救灾得到的经验教训和环境保护、生态平衡的要求,准备重新研究修改计划。为了寻求合理的计划方案,需要研究以下问题:(1)若按原计划填湖造地,水面的减少必然导致蓄水能力的下降。为了保证防洪能力不会下降,除了填湖费用外,还需要增加排水设备费用,所需经费与当年所填湖造地的面积x(亩)的平方成正比,其比例系数为a。又知每亩水面的年平均经济收益为b元,填湖造地后的每亩土地的年平均经济收益为c元(其中a,b,c均为常数)。若按原计划填湖造地,且使得今年的收益不小于支出,试求所填面积x的最大值。
(2)如果以每年1%的速度减少填湖造地的新增面积,并为保证水面的蓄洪能力和环保要求,填湖造地的总面积永远不能超过现有水面面积的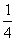 ,求今年填湖造地的面积最多只能占现有水面的百分之几?
,求今年填湖造地的面积最多只能占现有水面的百分之几?
解析:(1)收入不小于支出的条件可以表示为:cx-(ax2+bx)≥0
即ax2+(b-c)x≤0,x[ax-(c-b)] ≤0
当c-b≤0时,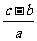 ≤x≤0,此时不能填湖造地
≤x≤0,此时不能填湖造地
当c-b>0时,0≤x≤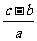 ,此时所填面积的最大值为
,此时所填面积的最大值为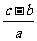 亩。
亩。
(2)设该县现有水面为m亩,今年填湖造地的面积为x亩,则x+(1-1%)x+(1-1%)2x+…+(1-1%)nx+…≤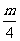
不等式左边是无穷等比数列的和,故有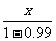 ≤
≤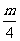 ,即x≤
,即x≤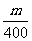 =0.25%m
=0.25%m
今年填湖造地的面积最多只能占有水面的0.25%。
[思维点拔]此列应用数极限解决实际问题。
6.等比数列{an}中,a1=-1,前n项和为Sn,若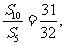 则
则 ………………………( )
………………………( )
(A)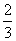 (B)-
(B)-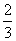 (C)2
(D)-2
(C)2
(D)-2
5.在等比数列中,a1>1,前项和Sn满足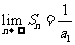 ,那么a1的取值范围是……………………( )
,那么a1的取值范围是……………………( )
(A)(1,+∞) (B)(1,4) (C)(1,2) (D)(1,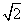 )
)
4.已知a、b都是实数,且a>0,如果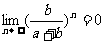 ,那么a与b的关系是………………( )
,那么a与b的关系是………………( )
A.a<2b
B.-a<2b
C.-a<b
D.-a<b<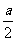
3.已知a、b、c是实常数,且 的值是………( )
的值是………( )
A.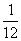 B.
B.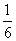 C.
C.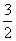 D.6
D.6
2、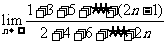 =_________________
=_________________
1、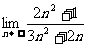 =
;
=
;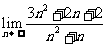 =
=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com