
5、f(x)=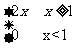 下面结论正确的是( )
下面结论正确的是( )
(A)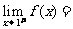
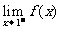 (B)
(B)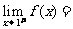 2 ,
2 ,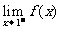 不存在
不存在
(C)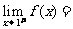 0,
0,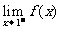 不存在
(D)
不存在
(D)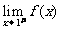 ≠
≠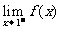
4、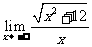 的值为( )
的值为( )
(A)1 (B)0 (C)-1 (D)±1
3、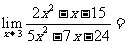 ( )
( )
(A)0
(B)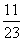 (C)-
(C)-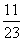 (D)不存在
(D)不存在
2、m<0,n>0时,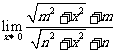 的值是( )
的值是( )
(A)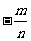 (B)0
(C)1
(D)
(B)0
(C)1
(D)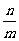
1、
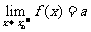 是函数在点xo处存在极限的( )
是函数在点xo处存在极限的( )
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件
2、函数的连续性
(1)函数连续性的概念:
①如果函数f(x)在x=x0处及其附近有定义,而且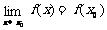 ,就说函数f(x)在x=x0处连续。
,就说函数f(x)在x=x0处连续。
注:函数f(x)在x=x0处连续必须具备三个条件:Ⅰ)函数f(x)在x=x0处及其附近有定义;Ⅱ)函数f(x)在x=x0处有极限;Ⅲ)函数f(x)在x=x0处的极限值等于这一点处的函数值f(x0)。
②右连续(或左连续):如果函数f(x)在x=x0处及其右侧(或左侧)有定义,而且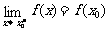 (或
(或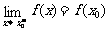 )。
)。
③若函数f(x)在(a,b)内每一点都连续,且在a点右连续,b点左连续,则称f(x)在闭区间[a,b]上连续。
注:函数f(x)在(a,b)内连续,只要求在(a,b)内每一点都连续即可,对在端点处是否连续不要求。
(2)函数连续性的运算:
①若f(x),g(x)都在点x0处连续,则f(x)±g(x),f(x)•g(x),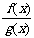 (g(x)≠0)也在点x0处连续。
(g(x)≠0)也在点x0处连续。
②若u(x)都在点x0处连续,且f(u)在u0=u(x0)处连续,则复合函数f[u(x)]在点x0处连续。
(3)初等函数的连续性:
①基本初等函数(指数函数,对数函数,三角函数等)在定义域里每一点处都连续。
②基本初等函数及常数经过有限次四则运送所得到的函数,都是初等函数,初等函数在其定义域里每一点处的极限都等于该点的函数值。
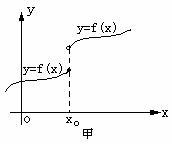 (3)
(3)
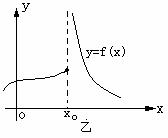
图甲表示的是f(x)在点x0处的左、右极限存在但不相等,即 不存在
不存在
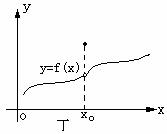
图乙表示的是f(x)在点x0处的左极限存在、右极限不存在,也属于 不存在
不存在
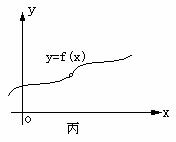
图丙表示的是 存在,但函数f(x)在点x0处没有定义
存在,但函数f(x)在点x0处没有定义
图丁表示的是 存在,但它不等于函数f(x)在点x0处的函数值。
存在,但它不等于函数f(x)在点x0处的函数值。
注意:函数f(x)在x=x0处连续与函数f(x)在x=x0处有极限的联系与区别。“连续必有极限,有极限未必连续。”
1、函数的极限
1) 当x→∞时函数f(x)的极限:
1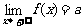 ;2
;2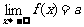 ; 3
; 3 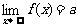
当自变量x取正值并且无限增大时,如果函数f(x)无限趋近于一个常数a,就说当x趋向于正无穷大时, 函数f(x)的极限是a,记作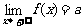 ,(或x→+∞时,f(x)→a)
,(或x→+∞时,f(x)→a)
当自变量x取负值并且无限增大时,如果函数f(x)无限趋近于一个常数a,就说当x趋向于负无穷大时, 函数f(x)的极限是a,记作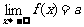 ,(或x→-∞时,f(x)→a)
,(或x→-∞时,f(x)→a)
注:自变量x→+∞和x→-∞都是单方向的,而x→∞是双向的,故有以下等价命题
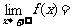
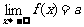
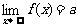
令 ,分别求
,分别求
2) 当x→x0时函数f(x)的极限:
1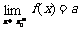 ; 2
; 2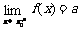 ; 3
; 3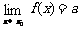
如果当x从点x=x0左侧(即x<x0)无限趋近于x0时,函数f(x)无限趋近于常数a。就说a是函数f(x)的左极限,记作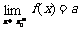 。
。
如果当x从点x=x0右侧(即x>x0)无限趋近于x0时,函数f(x)无限趋近于常数a。就说a是函数f(x)的右极限,记作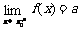 。
。
注:1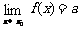 与函数f(x)在点x0处是否有定义及是否等于f(x0)都无关。
与函数f(x)在点x0处是否有定义及是否等于f(x0)都无关。
2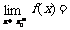
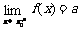
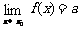 。并且可作为一个判断函数在一点处有无极限的重要工具。
。并且可作为一个判断函数在一点处有无极限的重要工具。
注:极限不存在的三种形态:①左极限不等于右极限
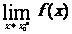 ;②
;②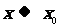 时,
时, ,③
,③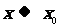 时,
时,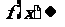 的值不唯一。
的值不唯一。
4)函数极限的运算法则:
若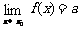 ,
,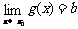 ,那么
,那么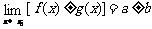 ;
;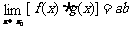 ;
;
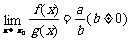 ;
;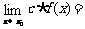
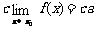 ;
;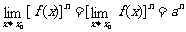 。
。
注:以上规则对于x→∞的情况仍然成立。
5)两个重要的极限: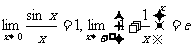 ;和一个法则:罗必塔法则:
;和一个法则:罗必塔法则: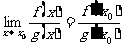
10.已知Sn=2+kan为数列的前n项和,其中k为不等于1的常数。
(1)求an; (2)若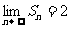 ,求k的取值范围.
,求k的取值范围.
9.求极限:
11. (05山东)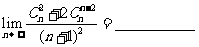
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com