
1.函数的导数实质是一个极限问题,不应理解为平均变化率,而是平均变化率的极限
例1、用定义求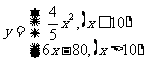 在点x=10处的导数。
在点x=10处的导数。
例2 求下列函数的导数:
(1)y=(2x2-1)(3x+1) (2)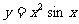 (3)
(3)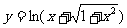
(4)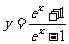 (5)
(5)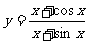 (6)
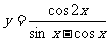
(6)
例3、已知曲线C: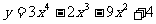
(1)求曲线C上横坐标为1的点的切线的方程;
(2)第(1)小题中切线与曲线C是否还有其它公共点。
例4(1)一球沿某一斜面自由滚下,测得滚下的垂直距离h(单位:m)与时间t(单位:s)之间的函数关系为h=t2,求t=4s时, 此球在垂直方向的瞬时速度.
(2)质点P在半径为10cm,圆心在原点的圆上逆时针做匀角速运动,角速度为1rad/s, 设该圆与x轴正半轴的交点A为起始点,求时刻t时,点P在y轴上射影点M的速度.
6.已知两曲线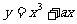 和
和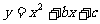 都经过点P(1,2),且在点P处有公切线,试求a,b,c值。
都经过点P(1,2),且在点P处有公切线,试求a,b,c值。
5.一质点的运动方程为s=5-3t2,则在一段时间[1,1+△t]内相应的平均速度为……( )
A. 3△t+6 B. -3△t +6 C. 3△t-6 D. -3△t-6
4.在曲线y=x2+1的图象上取一点(1,2)及邻近一点(1+△x,2+△y),则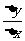 为……………( )
为……………( )
A.△x+ +2 B.△x-
+2 B.△x- -2
C.△x+2 D.2+△x-
-2
C.△x+2 D.2+△x-
3.如果一个质点由定点A开始运动,在时间t的位移函数为y=f(t)=t3+3,
(1)当t1=4,△t=0.01时,求△y和比值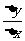 ;
(2)求t1=4时,
;
(2)求t1=4时,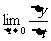 的值;
的值;
(3)说明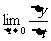 的几何意义.
的几何意义.
2.若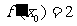 ,则
,则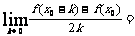
1.(05浙江)函数y=ax2+1的图象与直线y=x相切,则a=( )
(A)
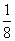 (B)
(B)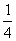 (C)
(C) 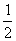 (D)1
(D)1
⒈导数的概念:
⑴曲线的切线;
⑵瞬时速度;
⑶导数的概念及其几何意义.
1.设函数 在
在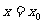 处附近有定义,当自变量在
处附近有定义,当自变量在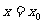 处有增量
处有增量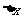 时,则函数
时,则函数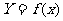 相应地有增量
相应地有增量 ,如果
,如果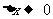 时,
时, 与
与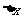 的比
的比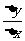 (也叫函数的平均变化率)有极限即
(也叫函数的平均变化率)有极限即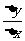 无限趋近于某个常数,我们把这个极限值叫做函数
无限趋近于某个常数,我们把这个极限值叫做函数 在
在 处的导数,记作
处的导数,记作 ,即:
,即: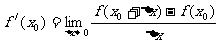
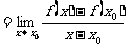
2函数 的导数
的导数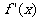 ,就是当
,就是当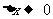 时,函数的增量
时,函数的增量 与自
与自
变量的增量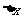 的比
的比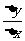 的极限,即
的极限,即
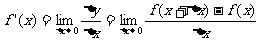 .
.
3函数 在点
在点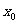 处的导数的几何意义,就是曲线
处的导数的几何意义,就是曲线 在点
在点
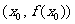 处的切线的斜率.
处的切线的斜率.
⒉常用的导数公式:
⑴ (C为常数); ⑵
(C为常数); ⑵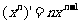 (
( );
);
⑶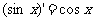 ; ⑷
; ⑷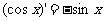 ;
;
⑸*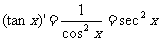 ; ⑹*
; ⑹*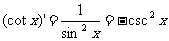 ;
;
⑺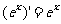 ; ⑻
; ⑻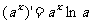 ;
;
⑼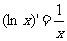 ;
⑽
;
⑽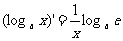 .
.
⒊导数的运算法则:
⑴两个函数四则运算的导数:
①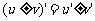 ;
②
;
②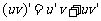 ;
③
;
③ .
.
⑵复合函数的导数: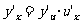 .
.
17.已知函数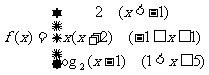
(1) 讨论f(x)在点x=-1,0,1处的连续性;(2)求f(x)的连续区间。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com