3、用“＞”“＜”“＝”填空：

(1)a<b<c<0则ac　　 bc ；　　 ；　　 ；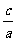

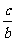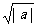
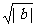(2) 0<a<b<c<1，则a^c　 b^c ；a^b　　 a^c；log_ca　　 log_cb；

algc　　 blgc；arcsina　　 arcsinb.

2、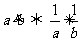成立的充要条件为 　　　　　　　

1、下列结论对否：

(　 )　　　 　　　　　(　 )

　　　　 (　 )　　　 　(　 )

　　 　　(　 )　　　 　　　　　(　 )

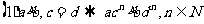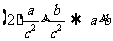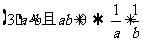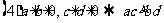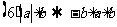3、不等式的基本性质

(1)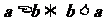(对称性)

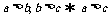(2)(传递性)

(3)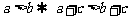(加法单调性)

(4)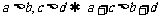(同向不等式相加)

(5)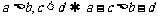(异向不等式相减)

(6)

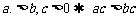
(7)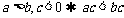(乘法单调性)

(8)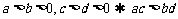(同向不等式相乘)

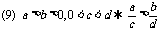(异向不等式相除)

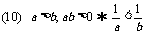(倒数关系)

(11)(平方法则)

(12)(开方法则)

2、两个实数的大小：

；；

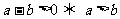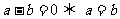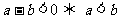
1、不等式的性质是解、证不等式的基础，对于这些性质，关键是正确理解和熟练运用，要

弄清每一个条件和结论，学会对不等式进行条件的放宽和加强。

13.(05重庆卷)设函数f(x)2x³3(a1)x²6ax8，其中aÎR。

　　 (1) 若f(x)在x3处取得极值，求常数a的值；

(2) 若f(x)在(¥,0)上为增函数，求a的取值范围。

12. (山东卷)已知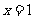是函数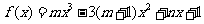的一个极值点，其中.

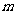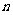(I)求与的关系式；

(II)求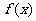的单调区间；

(III)当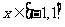时，函数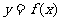的图象上任意一点的切线斜率恒大于3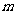，求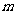的取值范围.

11.(05湖南卷)已知函数f(x)＝lnx，g(x)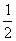＝ax²+bx，a≠0.

　 (Ⅰ)若b＝2，且h(x)＝f(x)－g(x)存在单调递减区间，求a的取值范围；

　 (Ⅱ)设函数f(x)的图象C₁与函数g(x)图象C₂交于点P、Q，过线段PQ的中点作x轴的垂线分别交C₁，C₂于点M、N，证明C₁在点M处的切线与C₂在点N处的切线不平行.

10. (05北京卷)过原点作曲线y＝e^x的切线，则切点的坐标为　　　 ；切线的斜率为　　 ．