
5、以下命题:⑴a>b |a|>b ⑵a>b
|a|>b ⑵a>b a2>b2 ⑶|a|>b
a2>b2 ⑶|a|>b  a>b ⑷a>|b|
a>b ⑷a>|b|  a>b
a>b
正确的个数有………………………………………………………………( )
(A) 1个 (B) 2个 (C) 3个 (D)4个
4、若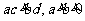 , …………………………………………………………( )
, …………………………………………………………( )
(A) 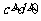 (B)
(B)
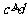 (C)
(C)
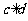 (D)c、d大小不确定
(D)c、d大小不确定
3、若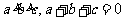 ,则有…………………………………………… ( )
,则有…………………………………………… ( )
(A) 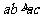 (B)
(B)
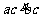 (C)
(C)
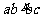 (D)以上皆错
(D)以上皆错
2、设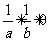 ,则 ………………………………………………………( )
,则 ………………………………………………………( )
(A) 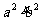 (B)
(B)
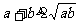 (C)
(C) 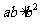 (D)
(D) 
1、下列命题中正确的是…………………………………………………… ( )
(A)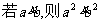 (B)
(B) 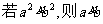 (C)
(C) 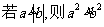 (D)
(D) 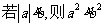
3、作差法是证明不等式的最基本也是很重要的方法,应引起高度注意.
2、处理分式不等式时不要随便将不等式两边乘以含有字母的分式,如果需要去分母,一定要考虑所乘的代数式的正负.
1、不等式的基本性质是解不等式与证明不等式的理论依据,必须透彻理解,特别要注意同向不等式可相加,也可相乘,但相乘时,两个不等式都需大于零.
例1、比较下面各小题中a与b的大小:
(1)a=m3-m2n-3mn2 与 b=2m2n-6mn2+n3 (2)a=3x2-x+1与b=2x2+x-1
(3)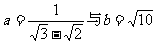 .
.
例2、a>0,a≠1,t>0,比较m=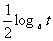 与n=
与n=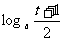 的大小.
的大小.
例3、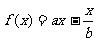 ,1≤
,1≤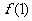 ≤2,13≤
≤2,13≤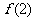 ≤20,求
≤20,求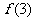 的取值范围.
的取值范围.
例4、设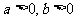 ,试比较
,试比较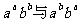 的大小。
的大小。
例5、已知f(lgx)=lg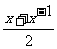 ,又设A=f(x+1),B=f(x)+f(1),试比较A、B的大小。
,又设A=f(x+1),B=f(x)+f(1),试比较A、B的大小。
4、已知A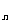 (n,a
(n,a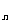 )为函数y=
)为函数y=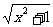 上的点,B
上的点,B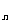 (n,b
(n,b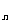 )为函数y=x上的点,其中n
)为函数y=x上的点,其中n N
N ,设c
,设c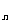 =a
=a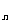 -b
-b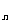 ,则c
,则c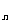 与c
与c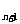 的大小关系为___________
的大小关系为___________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com