∴PQ⊥平面ABF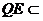，平面ABF，∴PQ⊥QF。

在RtΔPQF中，∠FPQ=60º，PF=2PQ。

∵PQ⊥AB，PQ⊥AF，，

在RtΔASB中，∴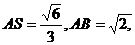

∴二面角A―DF―B的大小为60º。

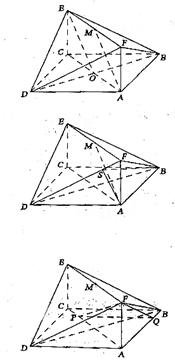
（3）设CP=t（0≤t≤2）,作PQ⊥AB于Q，则PQ∥AD，

∵AB⊥AF， AB⊥AD，

∴AB⊥平面ADF，∴AS是BS在平面ADF上的射影，

由三垂线定理得BS⊥DF。

∴∠BSA是二面角A―DF―B的平面角。

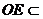∵平面BDE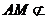， 平面BDE，∴AM∥平面BDE。

(2)在平面AFD中过A作AS⊥DF于S，连结BS，

18．方法一

解: (1)记AC与BD的交点为O,连接OE,

   ∵O、M分别是AC、EF的中点，ACEF是矩形，

∴四边形AOEM是平行四边形，∴AM∥OE。

又m+n=6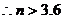,故在此次比赛中该选手至少打出了4个10环 .

故所求为1-0.4096-0.4096=0.1808                      

（3）设这次比赛中该选手打出了m个9环，n个10环

（2）