
2、在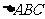 中,若
中,若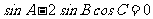 ,则
,则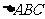 必定是
必定是
A、钝角三角形 B、锐角三角形 C、直角三角形 D、等腰三角形
1、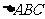 中,A、B的对边分别是
中,A、B的对边分别是 ,且
,且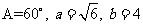 ,那么满足条件的
,那么满足条件的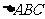
A、 有一个解 B、有两个解 C、无解 D、不能确定
例1、在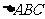 中,
中,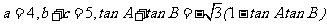 ,求
,求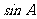 .
.
例2、在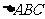 中,已知
中,已知 ,试判断
,试判断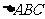 的形状.
的形状.
例3、已知A、C是三角形ABC的两个内角,且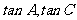 是方程
是方程 的两个实根。(1)求
的两个实根。(1)求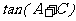 的值;(2)求
的值;(2)求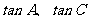 的取值范围;(3)求
的取值范围;(3)求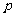 的取值范围.
的取值范围.
例4、已知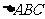 的三内角A、B、C成等差数列,且
的三内角A、B、C成等差数列,且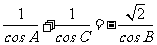 ,求
,求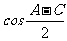 的值.
的值.
例5、(05湖南卷)已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A、B、C的大小.
5、在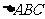 中,
中,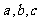 分别是角A、B、C所对的边,若
分别是角A、B、C所对的边,若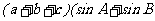
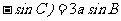 ,则
,则 = .
= .
4、在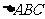 中,
中, 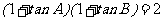 ,则
,则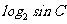 = .
= .
3、在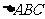 中,若
中,若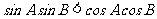 ,则
,则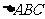 的形状为 .
的形状为 .
2、在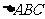 中,A>B是
中,A>B是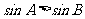 成立的 .条件.
成立的 .条件.
1、在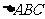 中,已知
中,已知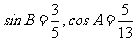 ,则
,则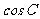 = .
= .
(二)、关于三角形内角的常用三角恒等式:
1.三角形内角定理的变形
由A+B+C=π,知A=π-(B+C)可得出:
sinA=sin(B+C),cosA=-cos(B+C).
而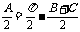 .有:
.有: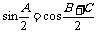 ,
,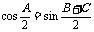 .
.
2.常用的恒等式:
(1)sinA+sinB+sinC=4cos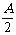 cos
cos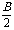 cos
cos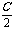 .
.
(2)cosA+cosB+cosC=1+4sin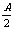 sin
sin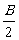 sin
sin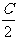 .
.
(3)sinA+sinB-sinC=4sin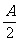 sin
sin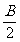 cos
cos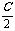 .
.
(4)cosA+cosB-cosC=-1+4cos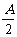 cos
cos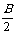 sin
sin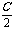 .
.
(5)sin2A+sin2B+sin2C=4sinAsinBsinC.
(6)cos2A+cos2B+cos2C=-1-4cosAcosBcosC.
(7)sin2A+sin2B+sin2C=2+2cosAcosBcosC.
(8)cos2A+cos2B+cos2C=1-2cosAcosBcosC.
(一).三角形中的各种关系
设△ABC的三边为a、b、c,对应的三个角为A、B、C.
1.角与角关系:A+B+C = π,
2.边与边关系:a + b > c,b + c > a,c + a > b,
a-b < c,b-c < a,c-a > b.
3.边与角关系:
1)正弦定理 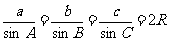
2)余弦定理 c2 = a2+b2-2bccosC,b2 = a2+c2-2accosB,a2 = b2+c2-2bccosA.
它们的变形形式有:a = 2R sinA,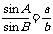 ,
,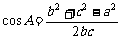 .
.
3)射影定理: a=b·cosC+c·cosB,
b=a·cosC+c·cosA,
c=a·cosB+c·cosA.
4)正切定理: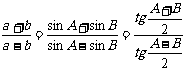
…………….(轮换)
5)模尔外得公式:
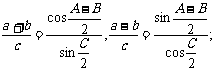
6)半角定理: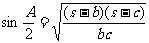
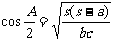
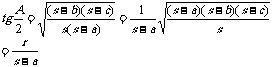
(以上公式均轮换)
7)面积公式:
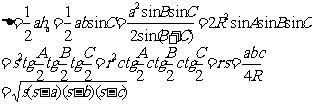
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com