
例1. 已知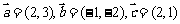 ,试求
,试求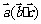 和
和 的值.
的值.
例2.已知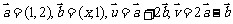 ,根据下列情况求
,根据下列情况求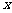 :
:
(1)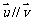 (2)
(2)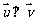
例3.已知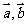 是两个非零向量,且
是两个非零向量,且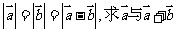 的夹角.
的夹角.
变题:已知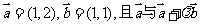 的夹角为锐角,求实数λ的取值范围.
的夹角为锐角,求实数λ的取值范围.
例4.已知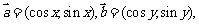
 与
与 之间有关系式
之间有关系式
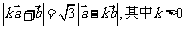
(1) 用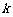 表示
表示 ;
;
(2) 求 的最小值,并求此时
的最小值,并求此时 与
与 的夹角
的夹角 的大小.
的大小.
基本训练:1、A 2、A 3、C 4、C 5、C
6、-4 7、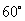
例题分析:例1、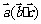 =(-8,-12),
=(-8,-12), =(-16,-8)
=(-16,-8)
例2、(1)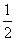 (2)-2或
(2)-2或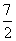
例3、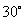
变题: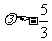 且
且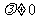
例4、(1)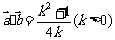 (2)最小值为
(2)最小值为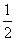 ,
,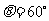
7.若向量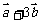 与
与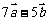 垂直,
垂直,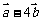 与
与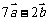 垂直,则非零向量
垂直,则非零向量 与
与 的夹角是 ______..
的夹角是 ______..
6.等腰Rt△ABC中,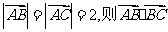 =
=
5.(04年重庆卷.文理6)若向量 与
与 的夹角为
的夹角为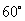 ,
,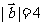 ,
,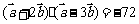 ,则向量
,则向量 的模为(
).
的模为(
).
A. 2 B. 4 C. 6 D. 12
4.(05江西卷)已知向量 ( )
( )
A.30° B.60° C.120° D.150°
3.已知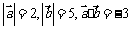 ,则
,则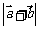 等于
( )
等于
( )
A. 23
B. 35
C. 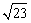 D.
D.
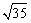
2.已知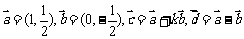 ,
, 与
与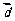 的夹角为
的夹角为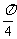 ,则
,则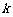 等于 ( )
等于 ( )
A. 1 B. 2 C. 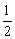 D.-1
D.-1
1.已知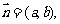 向量
向量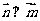 ,且
,且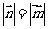 ,则
,则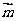 的坐标是
( )
的坐标是
( )
A.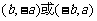 B.
B. 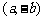 C.
C. 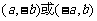 D.
D. 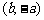
4.向量的数量积的运算律:
 ·b=b·
·b=b· ;(
;(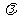
 )·b=
)·b=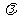 (
( ·b)=
·b)= ·(
·(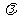 b);(
b);( +b)·c=
+b)·c= ·c+b·c.
·c+b·c.
3.向量的数量积的性质:
若 =(
=(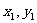 ),b=(
),b=(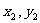 )则e·
)则e· =
= ·e=︱
·e=︱ ︱cos
︱cos (e为单位向量);
(e为单位向量);
 ⊥b
⊥b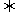
 ·b=0
·b=0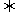
 (
( ,b为非零向量);︱
,b为非零向量);︱ ︱=
︱=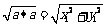 ;
;
cos =
=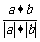 =
=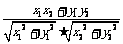 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com