1、(2002年北京高考题)64个直径都为的球，记它们的体积之和为，表面积之和为；一个直径为的球，记其体积为，表面积为，则(　　　 ) 　(A)　　　　　　 (B)　 　(C)　　　　　　 (D)　

例1．已知三棱锥内接于球, 三条侧棱两两垂直且长都为1, 求球的表面积与体积.

例2．在北纬圈上有甲、乙两地，它们的纬度圆上的弧长等于 (为地球半径)，求甲，乙两地间的球面距离。

例3．如图,球心到截面的距离为半径的一半，是截面圆的直径,是圆周上一点，是球的直径，

　　　 (1) 求证：平面平面；

　　　 (2) 如果球半径是，分为两部分, 且，求与所成的角；

(3) 如果，求二面角的大小。

例4.球面上三点组成这个球的一个截面的内接三角形，，

　　　 且球心到该截面的距离为球的半径的一半，

　　　 (1) 求球的体积；　　　 (2) 求两点的球面距离。

例5、从北京(北纬40⁰，东经120⁰)飞往南非首都约翰内斯堡(南纬30⁰，东径30⁰)有两条航线供其选择：甲航天线从北京沿纬度弧向西飞到希拉首都雅典(北纬40⁰，东径30⁰)，然后向南飞到目的地。乙航线：从北京向南飞到澳大利亚的珀斯(南纬30⁰，东径120⁰)，然后向西飞到目的地。间：哪一条航线较短？

1、(2002年北京高考题)64个直径都为的球，记它们的体积之和为，表面积之和为；一个直径为的球，记其体积为，表面积为，则(　 C　 ) 　(A)　　　　　　 (B)　 　(C)　　　　　　 (D)　 　2、一个圆锥的底面直径和高都同一个球的直径相等，那么圆锥与球的体积之比是(　 C　 ) 　(A)　　　　　　 (B)　　　　 (C)　　　　　 (D)　　　　　　　 　3、(1998年全国高考题)球面上有3个点，其中任意两点的球面距离都等于大圆周长的，经过这三个点的小圆的周长为4，那么这个球的半径为(　 B　 ) 　(A)　　　　　 (B) 　　　　(C)2　　　　　 (D)　　　　 　4、长方体的过一个顶点的三条棱长分别为3，4，5，且它的八个顶点都在同一个球面上，则这个球的表面积为(　　 D　　 ) 　(A)　　　　　 (B)　　 (C)　 　　　　(D) 　5、在北纬圈上有甲、已两地，甲地位于东径，乙地位于西径，则地球(半径为R)表面上甲、乙两地的最短距离为(　 D　　 ) 　(A)　　　　　　　 (B)　　　　　 (C)　　　　 (D)

球：⑴球的截面是一个圆面.

①球的表面积公式：.

②球的体积公式：.

⑵纬度、经度：

①纬度：地球上一点的纬度是指经过点的球半径与赤道面所成的角的度数.

②经度：地球上两点的经度差，是指分别经过这两点的经线与地轴所确定的二个半平面的二面角的度数，特别地，当经过点的经线是本初子午线时，这个二面角的度数就是点的经度.

(3). ①内切球：当四面体为正四面体时，设边长为a，，，

得.

注：球内切于四面体：

②外接球：球外接于正四面体，可如图建立关系式.

12、已知在四面体ABCD中，= a，= b，= c，G∈平面ABC．　　

　 (1)若G为△ABC的重心，试证明(a+b+c)；

　 (2)试问(1)的逆命题是否成立？并证明你的结论．

11．如图，已知三棱锥的侧面是底角为的等腰三角形，，且该侧面垂直于底面，，，，

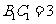(1)求证：二面角是直二面角；

(2)求二面角的正切值；

(3)若该三棱锥被平行于底面的平面所截，得到一个几何体，求几何体的侧面积．

10、三棱锥P-ABC中，PA=PB=PC=AB=AC=a，则该三棱锥表面积S的取值范围是　　　 　　；体积V的取值范围是　　　　　　 .

9、已知三棱锥A-BCD的体积为V，棱BC的长为a，面ABC和面DBC的面积分别为S₁和S₂，设面ABC和面DBC所成二面角为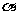，则＝　　　　　　 .

8、三棱锥的三条侧棱两两垂直，且长度分别为1cm,2cm,3cm，则此棱锥的体积为　　　　 。

7、正三棱锥的高是，侧棱长是，那么侧面和底面所成的二面角的大小是　　　　 .