
6.曲线关于直线对称问题:注意两点关于直线对称的条件:(1)两点连线与该直线垂直;(2)中点在此直线上.
5.关于相交弦的中点问题:涉及到弦的中点时,常结合韦达定理.
4.直线与圆锥曲线相交的弦长计算:(1)连结圆锥曲线上两点的线段称为圆锥曲线的弦;(2)易求出弦端点坐标时用距离公式求弦长;(3)一般情况下,解由直线方程和圆锥曲线方程组成的方程组,得到关于x(或y)的一元二次方程,利用方程组的解与端点坐标的关系,结合韦达定理得到弦长公式:|AB|=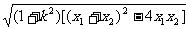 .
.
3.直线与圆锥曲线位置关系的判定:通法是消去一个未知数若得到的是关于另一未知数的一元二次方程,可用根的判别式 来判断,注意直线与圆锥曲线相切必有一个公共点,对圆与椭圆来说反之亦对,但对双曲线和抛物线来说直线与其有一公共点,可能是相交的位置关系.
来判断,注意直线与圆锥曲线相切必有一个公共点,对圆与椭圆来说反之亦对,但对双曲线和抛物线来说直线与其有一公共点,可能是相交的位置关系.
2.判断直线与圆锥曲线交点个数问题:即判断方程组解的个数.
1.关于直线与圆锥曲线的交点问题:一般方法是用解方程组的方法求其交点的坐标.
12.(江西卷)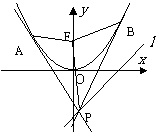 如图,设抛物线
如图,设抛物线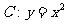 的焦点为F,动点P在直线
的焦点为F,动点P在直线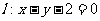 上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
(1)求△APB的重心G的轨迹方程.
(2)证明∠PFA=∠PFB.
11.过抛物线y2=4x的顶点O作任意两条互相垂直的弦OM、ON,求(1)MN与x轴交点的坐标;(2)求MN中点的轨迹方程
9.抛物线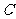 的顶点在坐标原点,对称轴为
的顶点在坐标原点,对称轴为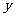 轴,
轴,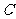 上动点
上动点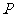 到直线
到直线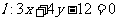 的最短距离为1,求抛物线
的最短距离为1,求抛物线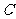 的方程。
的方程。
10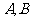 是抛物线
是抛物线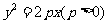 上的两点,且
上的两点,且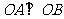 ,
,
(1)求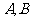 两点的横坐标之积和纵坐标之积;
两点的横坐标之积和纵坐标之积;
(2)求证:直线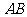 过定点;
过定点;
(3)求弦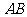 中点
中点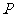 的轨迹方程;
的轨迹方程;
(4)求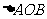 面积的最小值;
面积的最小值;
(5)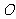 在
在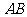 上的射影
上的射影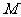 轨迹方程。
轨迹方程。
8.抛物线 的动弦
的动弦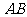 长为
长为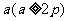 ,则弦
,则弦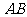 的中点
的中点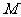 到
到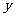 轴的最小距离为
。
轴的最小距离为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com