
(一)、定义法
例1.
⊙C: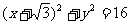 内部一点A(
内部一点A(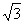 ,0)与圆周上动点Q连线AQ的中垂线交CQ于P,求点P的轨迹方程.
,0)与圆周上动点Q连线AQ的中垂线交CQ于P,求点P的轨迹方程.
例2.已知A(0,7)、B(0,-7),C(12,2),以C为焦点的椭圆经过点A、B,求此椭圆的另一个焦点F的轨迹方程.
5.已知椭圆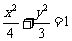 的两个焦点分别是F1,F2,P是这个椭圆上的一个动点,延长F1P到Q,使得|PQ|=|F2P|,求Q的轨迹方程是
.
的两个焦点分别是F1,F2,P是这个椭圆上的一个动点,延长F1P到Q,使得|PQ|=|F2P|,求Q的轨迹方程是
.
4.一动圆与圆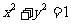 外切,而与圆
外切,而与圆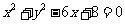 内切,则动圆圆心的轨迹方程是
内切,则动圆圆心的轨迹方程是
3.点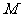 与点
与点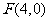 的距离比它到直线
的距离比它到直线 的距离小
的距离小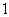 ,则点
,则点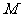 的轨迹方程是
的轨迹方程是
2. 若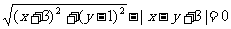 ,则点
,则点 的轨迹是( )
的轨迹是( )
 圆
圆
 椭圆
椭圆  双曲线
双曲线
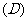 抛物线
抛物线
1.已知点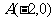 、
、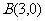 ,动点
,动点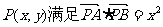 ,则点P的轨迹是( )
,则点P的轨迹是( )
 圆
圆  椭圆
椭圆  双曲线
双曲线  抛物线
抛物线
3.求动点轨迹的常用方法:直接法;定义法;代入法(相关点法);参数法.
2.求动点的轨迹的步骤:(1)建立坐标系,设动点坐标M(x,y);(2)列出动点M(x,y)满足的条件等式;(3)化简方程;(4)验证(可以省略);(5)说明方程的轨迹图形,最后“补漏”和“去掉增多”的点.
1.常见的轨迹:(1)在平面内,到两定点的距离相等的点的轨迹是连接两定点的线段的垂直平分线.(2)平面内到角的两边距离相等的点的轨迹是这个角的平分线.(3)平面内到定点的距离等于定长的点的轨迹是以定点为圆心的圆.(4)平面内到定点的距离与到定直线的距离之比等于常数的点的轨迹是圆锥曲线.当常数大于1时表示双曲线;当常数等于1时,表示抛物线;当常数大于0而小于1时表示椭圆.定点和定直线分别是圆锥曲线的焦点和相应的准线.(5)平面内到定直线的距离等于某一定值的点的轨迹是与这条直线平行的两条直线.
11. (05全国卷Ⅰ))已知椭圆的中心为坐标原点O,焦点在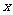 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,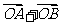 与
与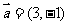 共线。
共线。
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且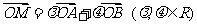 ,证明
,证明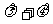 为定值。
为定值。
12设双曲线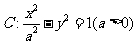 与直线
与直线 相交于两个不同的点
相交于两个不同的点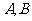 。
。
(1)求双曲线的离心率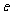 的取值范围;
的取值范围;
(2)设直线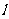 与
与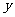 轴的交点为
轴的交点为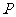 ,且
,且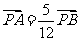 ,求
,求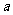 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com