6、 25.　 7、1152.　 8、 7.　　　 9、72..　　　 10、20.

12.三边长均为整数，且最大边长为11的三角形的个数是多少?

基本训练

1-5　 CBABD　　 6. 12　　 7. 48；9

同步练习答案：

1-3、 BACCB

11.五名学生报名参加四项体育比赛，每人限报一项，报名方法的种数为多少？又他们争夺这四项比赛的冠军，获得冠军的可能性有多少种？

10.设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的五个盒子.现将这五个球投放入这五个盒子内，要求每个盒子内投放一球，并且恰好有两个球的编号与盒子的编号相同，则这样的投放方法有多少种?

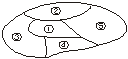
9.(2003年全国)如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色.现有4种颜色可供选择，则不同的着色方法共有_____________种.(以数字作答)

8.(2001年上海)某餐厅供应客饭，每位顾客可以在餐厅提供的菜肴中任选2菜2素共4种不同的品种.现在餐厅准备了5种不同的荤菜，若要保证每位顾客有200种以上的不同选择，则餐厅至少还需要不同的素菜品种_____________种.(结果用数值表示)

7.4棵柳树和4棵杨树栽成一行，柳树、杨树逐一相间的栽法有_____________种.

6.从1到10的正整数中，任意抽取两个相加，所得和为奇数的不同情形有__________种.

5.(05福建卷)从6人中选出4人分别到巴黎、伦敦、悉尼、莫斯科四个城市游览，要求每个城市有一人游览，每人只游览一个城市，且这6人中甲、乙两人不去巴黎游览，则不同的选择方案共有

　　　 A．300种　　　　　　　 B．240种　　　　　　　 C．144种　　　　　　　 D．96种

4.(2004年全国卷三.文理12)将4名教师分配到3所中学任教，每所中学至少1名教师，则不同的分配方案共有.　

A.12种　 B. 24种　 C. 36种　 D. 48种