
8.用数字0、1、2、3、4、5组成没有重复数字的四位数,
(1)可组成多少个不同的四位数?
(2)可组成多少个四位偶数?
(3)将(1)中的四位数按从小到大的顺序排成一数列,问第85项是什么?
7.在所有无重复数字的四位数中,千位上的数字比个位上的数字大2的数共有_______个.
6.三个人坐在一排八个座位上,若每人的两边都要有空位,则不同的坐法种数为__________.
5.(2004年四川模拟题)在由数字1,2,3,4,5组成的所有没有重复数字的5位数中,大于23145且小于43521的数共有_____________.
4.若m、n是不大于6的非负整数,则 表示不同的椭圆个数为
表示不同的椭圆个数为
A.A B.C
B.C C.A
C.A D.C
D.C
3.(2004年辽宁卷.12)有两排座位,前排11个座位,后排12个座位,现安排2人就座,规定前排中间的3个座位不能坐,并且这两人不左右相邻,那么不同的排法的种数是.
A. 234 B. 346 C. 350 D. 363
2.(2004年全国卷二.文理12)在由数字1,2,3,4,5组成的所有没有重复数字的5位数中,大于23145且小于43521的数共有.
A. 56个 B. 57个 C. 58个 D. 60个
1.5名成人带两个小孩排队上山,小孩不排在一起也不排在头尾,则不同的排法种数有
A.A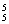 ·A
·A 种 B.A
种 B.A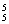 ·A
·A 种 C.A
种 C.A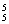 ·A
·A 种 D.A
种 D.A -4A
-4A 种
种
例1. 一条铁路原有m个车站,为适应客运需要,新增加n(n≥1,n∈N*)个车站,因而增加了58种车票(起迄站相同的车票视为相同的车票),问原来这条铁路有几个车站?现在又有几个车站?
例2. 从数字0、1、3、5、7中取出不同的三个作系数,可组成多少个不同的一元二次方程ax2+bx+c=0?其中有实数根的有几个?
剖析:(1)二次方程要求a不为0,故a只能在1、3、5、7中选,b、c没有限制.
(2)二次方程要有实根,需Δ=b2-4ac≥0,再对c分类讨论.
例3. 从0,1,2,3,4中取出不同的3个数字组成一个三位数,所有这些三位数的个位数字的和是多少?
深化拓展
从0,1,2,3,4,5,6,7,8,9中取出不同的5个数字组成一个5位偶数.(1)有多少个这样的数?(2)所有这些5位数的个位数字的和是多少?
答案:(1)A +C
+C C
C ·A
·A ;
;
(2)(2+4+6+8)C ·A
·A .
.
例4. (1)书架上有3本不同的书,如果保持这些书的相对顺序不变,再放上2本不同的书,有多少种不同的放法?
(2)身高均不相同的7个人排成一列,要求正中间的个子最高,从中间向两边看,一个比一个矮,有多少种不同的排法?
例5. 有4名男生、5名女生,全体排成一行,问下列情形各有多少种不同的排法?
(1)甲不在中间也不在两端;
(2)甲、乙两人必须排在两端;
(3)男、女生分别排在一起;
(4)男女相间;
(5)甲、乙、丙三人从左到右顺序保持一定.
6.若直线Ax+By=0的系数A、B可以从{0,2,3,4,5,6}中取不同的值.这些方程表示不同直线的条数是_____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com