
2.(2004年江苏,7)(2x+ )4的展开式中x3的系数是
)4的展开式中x3的系数是
A.6 B.12 C.24 D.48
1.已知(1-3x)9=a0+a1x+a2x2+…+a9x9,则|a0|+|a1|+|a2|+…+|a9|等于
A.29 B.49 C.39 D.1
3.利用二项式展开式可以证明整除性问题,讨论项的有关性质,证明组合数恒等式,进行近似计算等.
2.二项展开式的性质是解题的关键.
1.二项展开式的通项公式是解决与二项式定理有关问题的基础.
11.解法一:先取人,后取位子.
1,1,1,3:6人中先取3人有C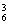 种取法,与剩余3人分到4所学校去有A
种取法,与剩余3人分到4所学校去有A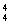 种不同分法,∴共C
种不同分法,∴共C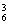 A
A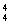 种分法;
种分法;
1,1,2,2:6人中取2人、2人、1人、1人的取法有C ·C
·C ·C
·C 种,然后分到4所学校去,有
种,然后分到4所学校去,有 种不同的分法,共C
种不同的分法,共C ·C
·C ·C
·C ·
· 种分法.所以符合条件的分配方法有C
种分法.所以符合条件的分配方法有C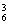 A
A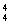 +C
+C ·C
·C ·C
·C ·
· =1560种.
=1560种.
解法二:先取位子,后取人.
1,1,1,3:取一个位子放3个人,有C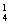 种取法,6人中分别取3人、1人、1人、1人的取法有C
种取法,6人中分别取3人、1人、1人、1人的取法有C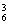 ·C
·C ·C
·C ·C
·C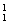 种,∴共有C
种,∴共有C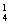 ·C
·C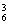 ·C
·C ·C
·C ·C
·C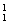 种.
种.
1,1,2,2:先取2个位子放2(其余2个位子放1)有C 种取法,6人中分别取2人,2人,1人,1人的取法有C
种取法,6人中分别取2人,2人,1人,1人的取法有C ·C
·C ·C
·C ·C
·C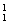 种,共有C
种,共有C ·C
·C ·C
·C ·C
·C ·C
·C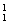 种.
种.
所以符合条件的分配方法有C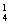 ·C
·C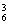 ·C
·C ·C
·C +C
+C ·C
·C ·C
·C ·C
·C =1560种.
=1560种.
10.解法一:依题意,给四部分涂色,至少要用两种颜色,故可分成三类涂色:
第一类,用4种颜色涂色,有A 种方法;
种方法;
第二类,用3种颜色涂色,选3种颜色的方法有C 种;在涂的过程中,选对顶的两部分(A、C或B、D)涂同色,另两部分涂异色有C
种;在涂的过程中,选对顶的两部分(A、C或B、D)涂同色,另两部分涂异色有C 种选法;3种颜色涂上去有A
种选法;3种颜色涂上去有A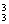 种涂法.共C
种涂法.共C ·C
·C ·A
·A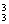 种涂法;
种涂法;
第三类,用两种颜色涂色.选颜色有C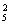 种选法;A、C与B、D各涂一色有A
种选法;A、C与B、D各涂一色有A 种涂法.共C
种涂法.共C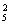 ·A
·A 种涂法.
种涂法.
所以共有涂色方法A +C
+C ·C
·C ·A
·A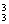 +C
+C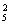 ·A
·A =260种.
=260种.
解法二:区域A有5种涂色法;区域B有4种涂色法;区域C的涂色法有2类:若C与A涂同色,区域D有4种涂色法;若C与A涂不同色,此时区域C有3种涂色法,区域D也有3种涂色法.
所以共有5×4×4+5×4×3×3=260种涂色法.
9.解:设这个团中有男人x人,则有女人18-x人,根据题意得C · C
· C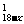 =64.解得x=10.
=64.解得x=10.
∴这个团中有男10人,女8人.
8. 解法一:添加的三个节目有三类办法排进去:①三个节目连排,有C A
A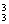 种方法;②三个节目互不相邻,有A
种方法;②三个节目互不相邻,有A 种方法;③有且仅有两个节目连排,有C
种方法;③有且仅有两个节目连排,有C C
C C
C A
A 种方法.根据分类计数原理共有C
种方法.根据分类计数原理共有C A
A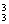 +A
+A +C
+C C
C C
C A
A =504种.
=504种.
解法二:从结果考虑,排好的节目表中有9个位置,先排入三个添加节目有A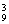 种方法,余下的六个位置上按6个节目的原有顺序排入只有一种方法.故所求排法为A
种方法,余下的六个位置上按6个节目的原有顺序排入只有一种方法.故所求排法为A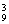 =504种.
=504种.
解法三: =504.
=504.
评述:插空法是处理排列、组合问题常用的方法.
5.把四位乘客当作4个元素作全排列有A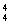 种排法,将一个空位和余下的4个空位作为一个元素插空有A
种排法,将一个空位和余下的4个空位作为一个元素插空有A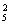 种排法.∴A
种排法.∴A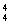 ·A
·A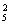 =480.
=480.
答案:480
例题分析
例1.解法一:问题分成三类:(1)甲、乙两人均不参加,有A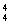 种;(2)甲、乙两人有且仅有一人参加,有2C
种;(2)甲、乙两人有且仅有一人参加,有2C (A
(A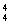 -A
-A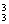 )种;(3)甲、乙两人均参加,有C
)种;(3)甲、乙两人均参加,有C (A
(A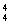 -2A
-2A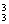 +A
+A )种.故共有252种.
)种.故共有252种.
解法二:六人中取四人参加的种数为A ,除去甲、乙两人中至少有一人不排在恰当位置的有C
,除去甲、乙两人中至少有一人不排在恰当位置的有C A
A 种,因前后把甲、乙两人都不在恰当位置的种数A
种,因前后把甲、乙两人都不在恰当位置的种数A 减去了两次.故共有A
减去了两次.故共有A -C
-C A
A +A
+A =252种.
=252种.
评述:对于带有限制条件的排列、组合综合题,一般用分类讨论或间接法两种方法处理.
例2.解:C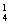 (C
(C C
C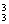 )A
)A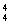 =576,第5次必测出一次品,余下3件在前4次被测出,从4件中确定最后一件品有C
=576,第5次必测出一次品,余下3件在前4次被测出,从4件中确定最后一件品有C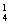 种方法,前4次中应有1正品、3次品,有C
种方法,前4次中应有1正品、3次品,有C C
C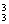 种,前4次测试中的顺序有A
种,前4次测试中的顺序有A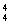 种,由分步计数原理即得.
种,由分步计数原理即得.
评述:本题涉及一类重要问题,即问题中既有元素的限制,又有排列的问题,一般是先选元素(即组合)后排列.
例3.解:依题意,A、B两种作物的间隔至少6垄,至多8垄.(1)间隔6垄时,有3×A 种;(2)间隔7垄时,有2×A
种;(2)间隔7垄时,有2×A 种.(3)间隔8垄时,有A
种.(3)间隔8垄时,有A 种.所以共有3A
种.所以共有3A +2A
+2A +A
+A =12种种植方法.
=12种种植方法.
例4.解法一:分类讨论法.
(1)前排一个,后排一个,2C ·C
·C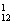 =192.
=192.
(2)后排坐两个(不相邻),
2(10+9+8+…+1)=110.
(3)前排坐两个,2·(6+5+…+1)+2=44个.
∴总共有192+110+44=346个.
解法二:考虑中间三个位置不坐,4号座位与8号座位不算相邻.
∴总共有A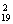 +2+2=346个.
+2+2=346个.
答案:B
评述:本题考查分类讨论在解排列组合应用题中的运用.这是一道难度较大的小综合题.
例5.解:(1)先将3人(用×表示)与4张空椅子(用□表示)排列如图(×□□×□□×),这时共占据了7张椅子,还有2张空椅子,一是分开插入,如图中箭头所示(↓×□↓□×□↓□×↓),从4个空当中选2个插入,有C 种插法;二是2张同时插入,有C
种插法;二是2张同时插入,有C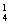 种插法,再考虑3人可交换有A
种插法,再考虑3人可交换有A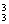 种方法.
种方法.
所以,共有A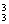 (C
(C +C
+C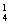 )=60(种).
)=60(种).
下面再看另一种构造方法:
先将3人与2张空椅子排成一排,从5个位置中选出3个位置排人,另2个位置排空椅子,有A C
C 种排法,再将4张空椅子中的每两张插入每两人之间,只有1种插法,所以所求的坐法数为A
种排法,再将4张空椅子中的每两张插入每两人之间,只有1种插法,所以所求的坐法数为A ·C
·C =60.
=60.
(2)可先让4人坐在4个位置上,有A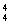 种排法,再让2个“元素”(一个是两个作为一个整体的空位,另一个是单独的空位)插入4个人形成的5个“空当”之间,有A
种排法,再让2个“元素”(一个是两个作为一个整体的空位,另一个是单独的空位)插入4个人形成的5个“空当”之间,有A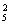 种插法,所以所求的坐法数为A
种插法,所以所求的坐法数为A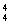 ·A
·A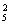 =480.
=480.
例6.证法一:由二项式定理(1+m)n=C m0+C
m0+C m1+…+C
m1+…+C mn,
mn,
(1+n)m=C n0+C
n0+C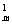 n1+…+C
n1+…+C ,
,
又因为C =
= ,C
,C =
= ,
,
而A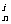 mi>A
mi>A ,所以C
,所以C m2>C
m2>C ,C
,C >C
>C n3,…,C
n3,…,C >C
>C .
.
又因为C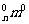 =C
=C ,C
,C =C
=C ,
,
所以(1+m)n>(1+n)m.
证法二:(1+m)n>(1+n)m
 nln(1+m)>mln(1+n)
nln(1+m)>mln(1+n)

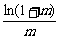 >
> .
.
令f(x)= ,x∈[2,+∞],
,x∈[2,+∞],
只要证f(x)在[2,+∞]上单调递减,只要证f ′(x)<0.
f ′(x)= =
=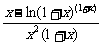 .
.
当x≥2时,x-lg(1+x)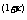 <0,
<0,
x2(1+x)>0,得f ′(x)<0,即x∈[2,+∞]时,f ′(x)<0.
以上各步都可逆推,得(1+m)n>(1+n)m.
作业:1-4 BBDBB 6. 42 7. 5
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com