
6.(2003年高考·新课程)A、B两个代表队进行乒乓球对抗赛,每队三名队员,A队队员是A1、A2、A3,B队队员是B1、B2、B3,按以往多次比赛的统计,对阵队员之间胜负概率如下:
|
对阵队员 |
A队队员胜的概率 |
A队队员负的概率 |
|
A1对B1 |
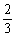 |
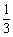 |
|
A2对B2 |
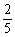 |
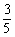 |
|
A3对B3 |
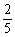 |
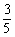 |
现按表中对阵方式出场,每场胜队得1分,负队得0分.设A队、B队最后所得总分分别为ξ、η.
(1)求ξ、η的概率分布;
(2)求Eξ、Eη.
5.(2004年天津,理18)从4名男生和2名女生中任选3人参加演讲比赛.设随机变量ξ表示所选3人中女生的人数.
(1)求ξ的分布列;
(2)求ξ的数学期望;
(3)求“所选3人中女生人数ξ≤1”的概率.
4.袋中有4只红球3只黑球,从袋中任取4只球,取到1只红球得1分,取到1只黑球得3分,设得分为随机变量ξ,则P(ξ≤6)=____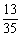 ____.
____.
3.现有一大批种子,其中优质良种占30%,从中任取5粒,记ξ为5粒中的优质良种粒数,则ξ的分布列是___ P(ξ=k)=C 0.3k0.75-k,k=0,1,…,5_____.
0.3k0.75-k,k=0,1,…,5_____.
2.一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,设停止时共取了ξ次球,则P(ξ=12)等于B
A.C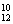 (
(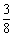 )10·(
)10·(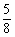 )2 B.C
)2 B.C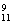 (
(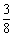 )9(
)9(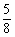 )2·
)2·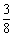
C.C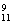 (
(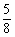 )9·(
)9·(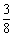 )2 D.C
)2 D.C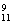 (
(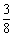 )9·(
)9·(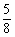 )2
)2
1.袋中有大小相同的5个球,分别标有1,2,3,4,5五个号码,现在在有放回抽取的条件下依次取出两个球,设两个球号码之和为随机变量ξ,则ξ所有可能取值的个数是B
A.5 B.9 C.10 D.25
[例1] 在10件产品中有2件次品,连续抽3次,每次抽1件,求:
(1)不放回抽样时,抽到次品数ξ的分布列;
(2)放回抽样时,抽到次品数η的分布列.
特别提示
求离散型随机变量分布列要注意两个问题:一是求出随机变量所有可能的值;二是求出取每一个值时的概率.
[例2] 一袋中装有5只球,编号为1,2,3,4,5,在袋中同时取3只,以ξ表示取出的三只球中的最小号码,写出随机变量ξ的分布列.
[例3] 盒中装有一打(12个)乒乓球,其中9个新的,3个旧的(用过的球即为旧的),从盒中任取3个使用,用完后装回盒中,此时盒中旧球个数ξ是一个随机变量,求ξ的分布列.
思考讨论
若本题改为:若每次取1个,用完放回再取1个,用完再放回,再取1个用完放回,则怎样求此时ξ的分布列呢?
[例4] (05年山东卷)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为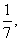 现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用
现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用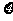 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
(I)求袋中所有的白球的个数;
(II)求随机变量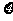 的概率分布;
的概率分布;
(III)求甲取到白球的概率.
〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓
5.设随机变量ξ-B(2,p),η-B(4,p),若P(ξ≥1)=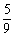 ,则P(η≥1)=__
,则P(η≥1)=__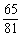 ____.
____.
*6.如果ξ-B(20,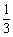 ),则使P(ξ=k)取最大值的k的值是________.
),则使P(ξ=k)取最大值的k的值是________.
解析: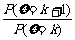 =
=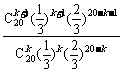 =
=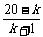 ×
×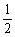 ≥1,
≥1,
得k≤6.
所以当k≤6时,P(ξ=k+1)≥P(ξ=k),
当k>0时,P(ξ=k+1)<P(ξ=k),
其中k=6时,P(ξ=k+1)=P(ξ=k),
从而k=6或7时,P(ξ=k)取得最大值.
答案:6或7
4.某批数量较大的商品的次品率为10%,从中任意地连续取出5件,其中次品数ξ的分布列为________.
|
ξ |
0 |
1 |
2 |
3 |
4 |
5 |
|
P |
0.95 |
0.5×0.94 |
0.1×0.93 |
0.01×0.92 |
4.5×0.14 |
0.15 |
3.已知随机变量ξ的分布列为P(ξ=k)=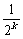 ,k=1,2,…,则P(2<ξ≤4)等于A
,k=1,2,…,则P(2<ξ≤4)等于A
A.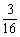 B.
B.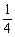 C.
C.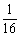 D.
D.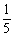
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com