
3.如图所示,细线拴一带负电的小球,球处在竖直向下的匀强
电场中,使小球在竖直平面内做圆周运动,则 ( )
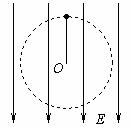 A.小球不可能做匀速圆周运动
A.小球不可能做匀速圆周运动
B.当小球运动到最高点时绳的张力一定最小
C.小球运动到最低点时,球的线速度一定最大
D.小球运动到最低点时,电势能一定最大
2.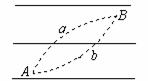 如图所示,平行的实线代表电场线,方向未知,电荷量为1×10-2C的正电荷在电场中只受电场力作用,该电荷由A点移到B点,动能损失了0.1 J,若A点电势为
如图所示,平行的实线代表电场线,方向未知,电荷量为1×10-2C的正电荷在电场中只受电场力作用,该电荷由A点移到B点,动能损失了0.1 J,若A点电势为
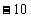 V,则 ( )
V,则 ( )
A.B点电势为零
B.电场线方向向左
C.电荷运动的轨迹可能是图中曲线a
D.电荷运动的轨迹可能是图中曲线b
1.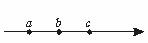 如图所示,a、b、c是一条电场线上的三点,电场线的方向由a到c,a、b间距离等于b、c间距离,用φa、φb、φc和Ea、Eb、Ec分别表示a、b、c三点的电势和场强,可以判定 ( )
如图所示,a、b、c是一条电场线上的三点,电场线的方向由a到c,a、b间距离等于b、c间距离,用φa、φb、φc和Ea、Eb、Ec分别表示a、b、c三点的电势和场强,可以判定 ( )
A.φa>φb>φc B.Ea>Eb>Ec
C.φa –φb=φb –φc D.Ea = Eb = Ec
2.偏转:当带点粒子垂直进入匀强电场时,带电粒子做类平抛运动
粒子在电场中的运动时间
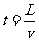
粒子在y方向获得的速度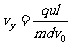
粒子在y方向的位移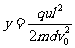
粒子的偏转角: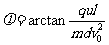
[例题解析]
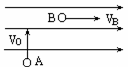 例1. 如图所示,质量为m,带电量为q的粒子,以初速度v0,从A点竖直向上射入真空中的沿水平方向的匀强电场中,粒子通过电场中B点时,速率vB=2v0,方向与电场的方向一致,则A,B两点的电势差为:
例1. 如图所示,质量为m,带电量为q的粒子,以初速度v0,从A点竖直向上射入真空中的沿水平方向的匀强电场中,粒子通过电场中B点时,速率vB=2v0,方向与电场的方向一致,则A,B两点的电势差为:

[解析]在竖直方向做匀减速直线运动2gh=v02①
电场力做正功、重力做负功,粒子的动能从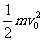 变为
变为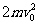 ,则
,则
根据动能定理
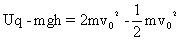

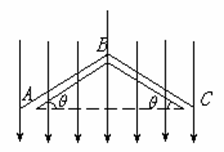 例2.一根对称的“八字”形玻璃管置于竖直平面内,如图所示。管所在的空间有竖直向下的匀强电场,电场强度E=1000牛/库。重力G=1.0×10-3牛,带电量Q= -2×10-6库的小物体在管内从A点由静止开始运动,它与管壁摩擦系数为0.5,管长AB=BC=3米,管的B处为一极短的光滑圆弧,管AB和BC与水平方向所夹的角度皆为37°,问
例2.一根对称的“八字”形玻璃管置于竖直平面内,如图所示。管所在的空间有竖直向下的匀强电场,电场强度E=1000牛/库。重力G=1.0×10-3牛,带电量Q= -2×10-6库的小物体在管内从A点由静止开始运动,它与管壁摩擦系数为0.5,管长AB=BC=3米,管的B处为一极短的光滑圆弧,管AB和BC与水平方向所夹的角度皆为37°,问
(1)小物体最终静止在何处?
(2)从A开始计算时,小物
体运动的总路程是多少?
[解析]A-B,作匀加速运动
B-C,作匀减速运动,
由于有机械能损失,到不了C点就停止,接
着返回作匀加速运动,过B点又作匀减速动, …最后停在B点.
由动能定理,对全过程,
L=AB=BC=3米
μ =0.5
(qE-mg)Lsin370- μ(qE-mg) cos370S=0
S=0.6 L /(0.5×0.8)
=1.8/0.4=4.5m
例3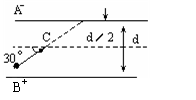 .1000eV的电子流在两极板中央斜向上方进入匀强电场,电场方向竖直向上,它的初速度与水平方向夹角为30°,如图为了使电子不打到上面的金属板上,应该在两金属板上加多大电压U?
.1000eV的电子流在两极板中央斜向上方进入匀强电场,电场方向竖直向上,它的初速度与水平方向夹角为30°,如图为了使电子不打到上面的金属板上,应该在两金属板上加多大电压U?
[解析]
电子流在匀强电场中做类似斜抛运动,欲使电子刚好不打金属板上,则必须使电子在d/2内竖直方向分速度减小到零,设此时加在两板间的电压为U,在电子流由C到A途中,
电场力做功We=EUAC,由动能定理
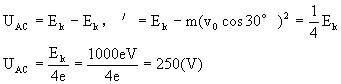
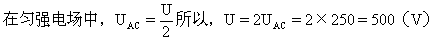
至少应加500V电压,电子才打不到上面金属板上。
例4、 如图,一个电子以速度v0=6.0×106m/s和仰角α=45°从带电平行板电容器的下板边缘向上板飞行。两板间场强E=2.0×104V/m,方向自下向上。若板间距离d=2.0×10-2m,板长L=10cm,问此电子能否从下板射至上板?它将击中极板的什么地方?
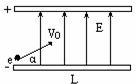
[解析]
应先计算y方向的实际最大位移,再与d进行比较判断。
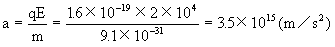
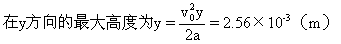
由于ym<d,所以电子不能射至上板。

因此电子将做一种抛物线运动,最后落在下板上,落点与出发点相距1.03cm。
小结:斜抛问题一般不要求考生掌握用运动学方法求解。用运动的合成分解的思想解此题,也不是多么困难的事,只要按照运动的实际情况把斜抛分解为垂直于电场方向上的的匀速直线运动,沿电场方向上的坚直上抛运动两个分运动。就可以解决问题。
例5、一个质量为m,带有电荷-q的小物块,可在水平轨道OX上运动,O端有一与轨道垂直的固定墙,轨道处于匀强电场中,场强大小为E,方向沿OX轴正方向,如图所示,小物体以初速v0
 从离O点为x0处沿OX轨道运动,运动时受到大小不变的摩擦
从离O点为x0处沿OX轨道运动,运动时受到大小不变的摩擦
力f
作用,且f<qE。设小物体与墙碰撞时不损失机械能且电量保持不变。
求它在停止运动前所通过的总路程s。
[解析]设小物块从开始运动到停止在O处的往复运动过程中位移为x0,往返路程为s。根据动能定理有
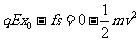
解得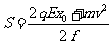
小结:本题考查两点内容一是要分析出物体最终停下来的位置,二是要学会能量分析。
例6、如图所示,在竖直平面内,光滑绝缘直杆AC与半径为R的圆周交于B、C两点,在圆心处有一固定的正点电荷,B为AC的中点,C点位于圆周的最低点。现有一质量为m、电荷量为-q、套在杆上的带负电小球从A点由 静止开始沿杆下滑。已知重力加速度为g,A点距过C点的水平面的竖直高度为3R,小球滑到B点时的速度大小为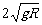 。求:
。求:
 (1)小球滑至C点时的速度的大小;
(1)小球滑至C点时的速度的大小;
(2)A、B两点的电势差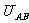 ;
;
(3)若以C点作为零电势点,试确定A点的电势。
[解析]
(1) B-C 3mgR/2=mvc2/2-mvB2/2
vc=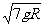
(2) A-B 3mgR/2+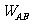 =mVB2/2-0
=mVB2/2-0
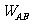 =mgR/2
=mgR/2
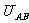 =
=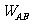 /q=mgr/-2q
/q=mgr/-2q
(3) 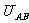 =
=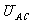 =-mgR/2q=
=-mgR/2q=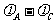
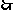
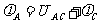 =-mgR/2q
=-mgR/2q
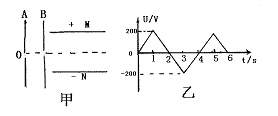 例7、如图甲所示,A、B为两块靠得很近的平行金属板,板中央均有小孔。一束电子以初动能Ek=120ev,从A板上的小孔O不断垂直于板射入A、B之间,在B板右侧,平行金属板的板长L=2×10-2m,板间距离d=4×10-3m,两板上所加电压为U2=20V。现在在A、B两板上加一个如图乙所示的变化电压U1,在t=0到t=2s时间内,A板电势高于B板,则在U1随时间变化的第一个周期内
例7、如图甲所示,A、B为两块靠得很近的平行金属板,板中央均有小孔。一束电子以初动能Ek=120ev,从A板上的小孔O不断垂直于板射入A、B之间,在B板右侧,平行金属板的板长L=2×10-2m,板间距离d=4×10-3m,两板上所加电压为U2=20V。现在在A、B两板上加一个如图乙所示的变化电压U1,在t=0到t=2s时间内,A板电势高于B板,则在U1随时间变化的第一个周期内
(1)电子在哪段时间内可以从B板小孔射出?
(2)在哪段时间内,电子能从偏转电场右侧飞出?
(由于A、B两板距离很近,可以认为电子穿过A、B板间所用时间很短,可以不计)
[解析](1)能射出B板,要求电子达到B板时速度大于或等于零,由动能定理得

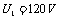
AB两板所加电压在0-1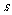 区间里
区间里
有U=200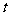 故
故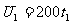
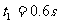
由于电压图像的对称性,另一对应时
刻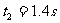 在下半周期,电场力做正功电子均能射出,所以能射出的时间段为0-
在下半周期,电场力做正功电子均能射出,所以能射出的时间段为0- 及
及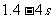
(2)设电子从偏转电场中垂直射入时速度为 ,那么侧移是
,那么侧移是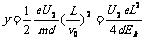
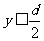 才能射出
才能射出 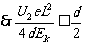
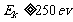 又
又
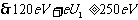
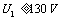 又因
又因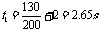
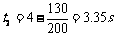 所以在
所以在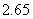 -
-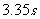 内有电子射出。
内有电子射出。
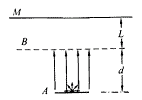
例8、如图所示,在厚铅板A表面中心放置一很小的放射源,可向各个方向放射出速率为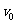 的
的 粒子(质量为m,电量为q),在金属网B与A板间加有竖直向上的匀强电场,场强为E,A与B间距为d,B网上方有一很大的荧光屏M,M与B间距为L,当有
粒子(质量为m,电量为q),在金属网B与A板间加有竖直向上的匀强电场,场强为E,A与B间距为d,B网上方有一很大的荧光屏M,M与B间距为L,当有 粒子打在荧光屏上时就能使荧光屏产生一闪光点。整个装置放在真空中,不计重力的影响,试分析:
粒子打在荧光屏上时就能使荧光屏产生一闪光点。整个装置放在真空中,不计重力的影响,试分析:
 (1)打在荧光屏上的
(1)打在荧光屏上的 粒子具有的动能有多大?
粒子具有的动能有多大?
(2)荧光屏上闪光点的范围有多大?
(3)在实际应用中,往往是放射源射出的 粒子
粒子
的速率未知,请设计一个方案,用本
装置来测定 粒子的速率。
粒子的速率。
[解析](1) 粒子在电场中作加速运动,电场力作正功,
粒子在电场中作加速运动,电场力作正功,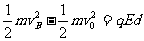
打在荧光屏上的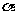 粒子且有动能,
粒子且有动能,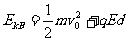
(2)当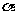 粒子初速度与电场线垂直时,作类平抛运动,沿电场线方向
粒子初速度与电场线垂直时,作类平抛运动,沿电场线方向
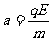
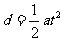
到达B板所用时间为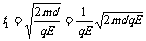
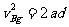
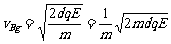
从B板到达M板所用时间为
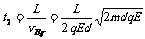
粒子运动总时间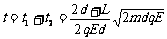
荧光屏上闪光范围是一个圆,其半径R=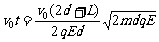
(3)由前问题可知,荧光屏上闪光范围是一个圆,其半径与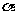 粒子的初速度成正比。
粒子的初速度成正比。
测得圆的半径R,可计算出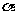 粒子的初速度
粒子的初速度 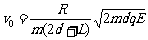
或将AB间电场反向,电场力对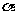 粒子做负功,逐渐增大电场强度,当荧光屏上闪光消失时,
粒子做负功,逐渐增大电场强度,当荧光屏上闪光消失时,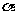 粒子初动能全部用来克服电场力做功。
粒子初动能全部用来克服电场力做功。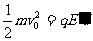

[专题训练与高考预测]
1.加速: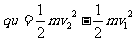
2.电容
(1)定义:电容器所带的电荷量Q与电容器两极板间的电势差U的比值
表达式: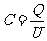
(2)平行板电容器电容公式: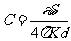
1.电容器
任何两个彼此绝缘又相隔很近的导体都可以看成是一个电容器。(最简单的电容器是平行板电容器,金属板称为电容器的两个极板,绝缘物质称为电介质)
4.电场力做功
(1)电场力做功与电荷电势能变化的关系:
电场力对电荷做正功,电荷电势能减少;电场力对电荷做负功,电荷电势能增加。电势能增加或减少的数值等于电场力做功的数值。
(2)电场力做功的特点:
电荷在电场中任意两点间移动时,它的电势能的变化量势确定的,因而移动电荷做功的 值也势确定的,所以,电场力移动电荷所做的功与移动的路径无关,仅与始末位置的电势差由关,这与重力做功十分相似。
3.等势面
(1)定义:电场中电势相等的点构成的面。
(2)特点:一是在同一等势面上的各点电势相等,所以在同一等势面上移动电荷,电场力不做功二是电场线一定跟等势面垂直,并且由电势高的等势面指向电势低的等势面。
2.电势
(1)电势是表征电场性质的重要物理量,通过研究电荷在电场中的电势能与它的电荷量的比值得出。
(2)公式: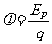 (与试探电荷无关)
(与试探电荷无关)
(3)电势与电场线的关系:电势顺线降低。
(4)零电势位置的规定:电场中某一点的电势的数值与零电势点的选择无关,大地或无穷远处的电势默认为零。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com