
1.某电子以固定的正电荷为圆心在匀强磁场中做匀速圆周运动,磁场方向垂直于它的运动平面,电子所受电场力恰好是磁场对它作用力的3倍.若电子电量为e,质量为m,磁感应强度为B.那么,电子运动的角速度可能是 ( )
A.4Be/m B.3Be/m C.2Be/m D.Be/m
复合场是指重力场、电场和磁场三者或其中任意两者共存于同一区域的场;组合场是指电场与磁场同时存在,但不重叠出现在同一区域的情况.带电体在复合场中的运动(包括平衡),说到底仍然是一个力学问题,只要掌握不同的场对带电体作用的特点和差异,从分析带电体的受力情况和运动情况着手,充分发掘隐含条件,建立清晰的物理情景,最终把物理模型转化成数学表达式,即可求解.
解决复合场或组合场中带电体运动的问题可从以下三个方面入手:1、动力学观点(牛顿定律结合运动学方程);2、能量观点(动能定理和机械能守恒或能量守恒);3、动量观点(动量定理和动量守恒定律).
一般地,对于微观粒子,如电子、质子、离子等不计重力,而一些实际物体,如带电小球、液滴等应考虑其重力.有时也可由题设条件,结合受力与运动分析,确定是否考虑重力.
 [例题解析]
[例题解析]
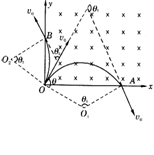
例1.如图所示,在第I象限范围内有垂直xOy平面的匀强磁场,
磁感应强度为B,质量为m,电荷量为q的带电粒子(不计重
力),在xOy平面内经原点O射入磁场中,初速度为v0,且与
x轴成600,试分析并计算:
(1)带电粒子从何处离开磁场?穿越磁场时运动方向发生的偏
转角多大?
(2)带电粒子在磁场中运动时间多长?
[解析](1)带电粒子带负电荷,进入磁场后将向x轴偏转,从A点离开磁场;若带正电荷,进入磁场后将向y轴偏转,从B点离开磁场,如图所示。带电粒子进入磁场后做匀速圆周运动,轨迹半径均为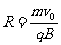 ,圆心位于过O与v0垂直的同一条直线上,O1O=O2O=O1A=O2B=R。带电粒子沿半径为R的圆周运动一周所花时间
,圆心位于过O与v0垂直的同一条直线上,O1O=O2O=O1A=O2B=R。带电粒子沿半径为R的圆周运动一周所花时间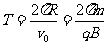 。
。
(1)带负电荷的粒子从x轴上的A点离开磁场,运动方向发生的偏转角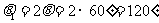 ;A点到原点O的距离
;A点到原点O的距离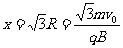 。
。
 粒子若带正电荷 ,在y轴上的B点离开磁场,运动方向发生的偏转角
粒子若带正电荷 ,在y轴上的B点离开磁场,运动方向发生的偏转角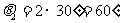 ,B点到原点O的距离
,B点到原点O的距离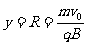 。
。
(2)粒子若带负电,它从O点运动到A点所花时间
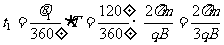 。
。
粒子若带正电荷,它从O点运动到B点所花时间
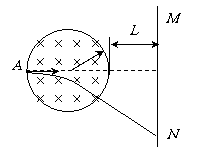
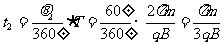 。
。
例2.圆心为O、半径为r的圆形区域中有一个磁感强度为 B、
方向为垂直于纸面向里的匀强磁场,与区域边缘的最短距
离为L的O'处有一竖直放置的荧屏MN,今有一质量为
m的电子以速率v从左侧沿OO'方向垂直射入磁场,越
出磁场后打在荧光屏上之P点,如图所示,求O'P的长度和电子通过磁场所用的时间。
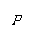 [解析]电子所受重力不计。它在磁场中做匀速圆周运动,圆心为O″,半径为R。圆弧段轨迹AB所对的圆心角为θ,电子越出磁场后做速率仍为v的匀速直线运动, 如图4所示,连结OB,∵△OAO″≌△OBO″,又OA⊥O″A,故OB⊥O″B,由于原有BP⊥O″B,可见O、B、P在同一直线上,且∠O'OP=∠AO″B=θ,在直角三角形OO'P中,O'P=(L+r)tanθ,而
[解析]电子所受重力不计。它在磁场中做匀速圆周运动,圆心为O″,半径为R。圆弧段轨迹AB所对的圆心角为θ,电子越出磁场后做速率仍为v的匀速直线运动, 如图4所示,连结OB,∵△OAO″≌△OBO″,又OA⊥O″A,故OB⊥O″B,由于原有BP⊥O″B,可见O、B、P在同一直线上,且∠O'OP=∠AO″B=θ,在直角三角形OO'P中,O'P=(L+r)tanθ,而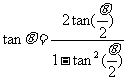 ,
,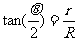 ,所以求得R后就可以求出O'
,所以求得R后就可以求出O' P了,电子经过磁场的时间可用t=
P了,电子经过磁场的时间可用t=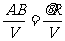 来求得。
来求得。
由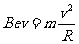 得R=
得R=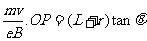
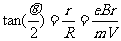 ,
,
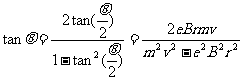
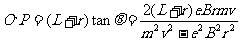 ,
,
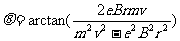
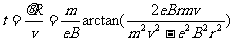
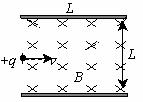 例3.长为L的水平极板间,有垂直纸面向内的匀强磁场,如图所示,磁感强度为B,板间
例3.长为L的水平极板间,有垂直纸面向内的匀强磁场,如图所示,磁感强度为B,板间
距离也为L,板不带电,现有质量为m,电量为q的带正电粒
子(不计重力),从左边极板间中点处垂直磁感线以速度v水平
射入磁场,欲使粒子不打在极板上,可采用的办法是:
A.使粒子的速度v<BqL/4m;
B.使粒子的速度v>5BqL/4m;
C.使粒子的速度v>BqL/m;
 D.使粒子速度BqL/4m<v<5BqL/4m。
D.使粒子速度BqL/4m<v<5BqL/4m。
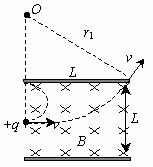
[解析]由左手定则判得粒子在磁场中间向上偏,而作匀速圆
周运动,很明显,圆周运动的半径大于某值r1时粒子可以从极
板右边穿出,而半径小于某值r2时粒子可从极板的左边穿出,
现在问题归结为求粒子能在右边穿出时r的最小值r1以及粒子
在左边穿出时r的最大值r2,由几何知识得:
粒子擦着板从右边穿出时,圆心在O点,有:
r12=L2+(r1-L/2)2得r1=5L/4,
又由于r1=mv1/Bq得v1=5BqL/4m,∴v>5BqL/4m时粒子能从右
边穿出。
粒子擦着上板从左边穿出时,圆心在O'点,有r2=L/4,又由r2=mv2/Bq=L/4得v2=BqL/4m
∴v2<BqL/4m时粒子能从左边穿出。
综上可得正确答案是A、B。
例4.如图所示,匀强电场方向水平向右,匀强磁场方向垂直于纸面向里,一质量为m、带电荷量为q的粒子以速度v与磁场垂直、与电场成450射入复合场中,恰能做匀速直线运动。求电场强度E的大小、磁感应强度B的大小。
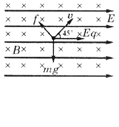 [解析]由于带电粒子所受洛伦兹力与v垂直,电场力方向与电场线平行,知粒子必须还受重力才能做匀速直线运动。假设粒子带负电受电场力水平向左,则它受洛伦兹力f就应斜向右下与v垂直,这样粒子不能做匀速直线运动,所以粒子应带正电,画出受力分析图根据合外力为零可得
[解析]由于带电粒子所受洛伦兹力与v垂直,电场力方向与电场线平行,知粒子必须还受重力才能做匀速直线运动。假设粒子带负电受电场力水平向左,则它受洛伦兹力f就应斜向右下与v垂直,这样粒子不能做匀速直线运动,所以粒子应带正电,画出受力分析图根据合外力为零可得
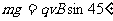 ①
①
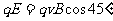 ②
②
由①式得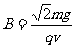 ,由①②得
,由①②得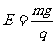
评析 正确分析带电粒子的受力情况,抓住“匀速直线运动”,归结到力的平衡问题。
例5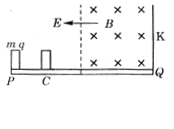 .如图所示,PQ为一块长为l、水平放置的绝缘平板,整个空间存在着水平向左的匀强电场,板的右半部分还存在着垂直于纸面向里的有界匀强磁场。一质量为m、带电荷量为q的物体,从板左端P由静止开始做匀加速运动,进入磁场后恰做匀速运动,碰到右端带控制开关K的挡板后被弹回,且电场立即被撤消,物体在磁场中仍做匀速运动,离开磁场后又做匀减速运动,最后停在C点,已知PC=
.如图所示,PQ为一块长为l、水平放置的绝缘平板,整个空间存在着水平向左的匀强电场,板的右半部分还存在着垂直于纸面向里的有界匀强磁场。一质量为m、带电荷量为q的物体,从板左端P由静止开始做匀加速运动,进入磁场后恰做匀速运动,碰到右端带控制开关K的挡板后被弹回,且电场立即被撤消,物体在磁场中仍做匀速运动,离开磁场后又做匀减速运动,最后停在C点,已知PC=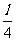 ,物体与板间动摩擦间数为
,物体与板间动摩擦间数为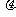 ,求:
,求:
(1)物体带何种电荷?
(2)物体与板碰撞前后的速度v1和v2
(3)电场强度E和磁感应强度B各多大?
[解析](1)物体带负电。
(2)因碰前匀速,有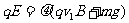 ,碰后先匀速,有
,碰后先匀速,有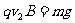 ,再减速最后停在C点,从P到进入磁场的过程中,用动能定理,有
,再减速最后停在C点,从P到进入磁场的过程中,用动能定理,有
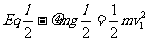
从出磁场到C点,用动能定理
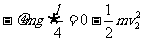
求得 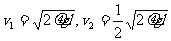
(3)由(2)可知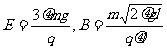
评析 解决问题的关键之一是弄清物理过程,这样就不难找到解决问题的方法。
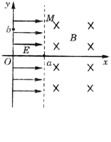 例6.如图所示,在平面直角坐标系xOy平面内,x<0的区域内没有电场和磁场;
例6.如图所示,在平面直角坐标系xOy平面内,x<0的区域内没有电场和磁场;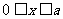 区域内有一匀强电场区,电场方向沿x轴正方向;x=0处的各点电势为零,x=a处各点电势为
区域内有一匀强电场区,电场方向沿x轴正方向;x=0处的各点电势为零,x=a处各点电势为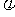 a,在x>a处充满匀强磁场,磁场方向垂直于xOy平面向里。现有一带电粒子,质量为m,电荷量为q,在x=0,y=0的位置由静止开始自由释放,求:
a,在x>a处充满匀强磁场,磁场方向垂直于xOy平面向里。现有一带电粒子,质量为m,电荷量为q,在x=0,y=0的位置由静止开始自由释放,求:
(1)靶子M的坐标是x=a,y=b,带电粒子击中靶子时的速度多大?
(2)磁感应强度为多大时,带电粒子才能击中靶子M?
[解析](1)带电粒子从原点由静止释放后,在 的匀强电场
的匀强电场
区域内被加速,由动能定理得
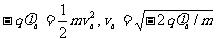 ,
,
va即为进入匀强磁场时速度的大小。
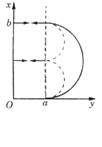 进入匀强磁场区内带电粒子做匀速圆周运动,速度大小恒定不变,所
进入匀强磁场区内带电粒子做匀速圆周运动,速度大小恒定不变,所
以击中靶子M的速度大小为 。
。
(2)带电粒子可以经电场、磁场各一次后击中靶子,也可能经电场、
磁场多次后才击中靶子,如图6-18所示,故轨道半径R有多个值,
对应的磁感应强度B也有多个可能值。设带电粒子在磁场中经n(n=1,
2,3,……)次偏转后击中靶子M。
根据题意有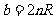 ①
①
洛伦兹力提供粒子做圆周运动的向心力,由牛顿第二定律,
有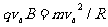 ②
②
由①②解得磁感应强度的可能值
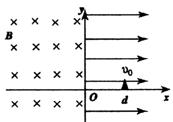
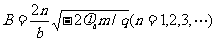
评析 正确理解题意,挖掘隐含条件--粒子在电场和磁
场中可能的重复性和对称性,从而求出正确的结果。
例7、如图所示,在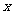 >0的空间中,存在沿
>0的空间中,存在沿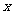 轴方向的匀强电
轴方向的匀强电
场,电场强度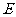 =10N/C;在x<0的空间中,存在垂直xy
=10N/C;在x<0的空间中,存在垂直xy
平面方向的匀强磁场,磁感应强度B=0.5T。一带负电的
粒子(比荷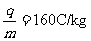 )在x=0.06m处的d点以
)在x=0.06m处的d点以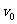 =
=
8m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力。求:
(1)带电粒子开始运动后第一次通过y轴时距O点的距离。
(2)带电粒子进入磁场后经多长时间返回电场。
(3)带电粒子运动的周期。
[解析](1)对于粒子在电场中的运动有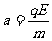 ,
,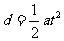 ,第一次通过y轴的交点到O点的距离为
,第一次通过y轴的交点到O点的距离为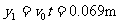 ;
;
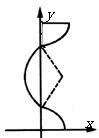 (2)x方向的速度
(2)x方向的速度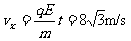 ,设进入磁场时速度与y轴正方向的夹角为
,设进入磁场时速度与y轴正方向的夹角为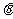 ,
,
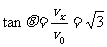 ,故
,故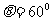 ,所以在磁场中作圆周运动所对
,所以在磁场中作圆周运动所对
应的圆心角为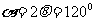 ,带电粒子在磁场中做匀速圆周运
,带电粒子在磁场中做匀速圆周运
动周期为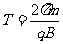 ,带电粒子在磁场中运动的时间
,带电粒子在磁场中运动的时间
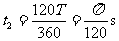 ;
;
(3)从开始至第一次到达y轴的时间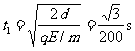 ,从磁场再次回到电场中的过程(未进入第二周期)是第一次离开电场时的逆运动,根据对称性
,从磁场再次回到电场中的过程(未进入第二周期)是第一次离开电场时的逆运动,根据对称性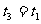 ,因此粒子的运动周期为
,因此粒子的运动周期为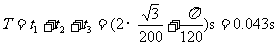 。
。
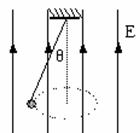 例8、在空间同时存在匀强磁场和匀强电场,匀强电场方向竖直向上,场强大小为E,匀强磁场方向和大小均未知,如图所示。现有一质量为m的带电小球,用长为L的绝缘线悬挂在一点,小球在水平面上以角速度ω作匀速圆周运动,顺着电场线方向观察,角速度为顺时针旋转,这时线与竖直方向夹角为θ,线上拉力为零。
例8、在空间同时存在匀强磁场和匀强电场,匀强电场方向竖直向上,场强大小为E,匀强磁场方向和大小均未知,如图所示。现有一质量为m的带电小球,用长为L的绝缘线悬挂在一点,小球在水平面上以角速度ω作匀速圆周运动,顺着电场线方向观察,角速度为顺时针旋转,这时线与竖直方向夹角为θ,线上拉力为零。
(1)小球带何种电荷?电量为多少?
(2)磁感应强度B的大小和方向分别是什么?
(3)突然撤去磁场,小球将怎样运动?这时线上拉力多大? [解析](1)绳子上拉力为零,说明电场力和重力平衡,可知小球带正电,洛仑兹力提供向心力,可知磁感应强度方向竖直向下。由qE=mg得q=mg/E.
(2)由牛顿第二定律有BqV=mV2/R得B=mV/qR=ωE/g。
(3)突然撤去磁场,重力仍与重力平衡,小球要以此时的速度作匀速直线运动,但瞬间绳子产生弹力,迫使小球在速度方向和绝缘线决定的平面上做匀速圆周运动,由于小球的速度大小不变,所以线上的拉力大小T=mV2/L=m(ωLsinθ)2/L=mLω2sin2θ。
例9、质谱仪主要用于分析同位素, 测定其质量、荷质比和含量比, 如图所示为一种常用的质谱仪, 由离子源O、加速电场U、速度选择器E、B1和偏转磁场B2组成。某种粒子无初速从粒子源进入加速电场,并测出该粒子在偏转磁场的轨道直径为d,若已知速度选择器E、B1和偏转磁场B2,求(1)此粒子的荷质比;(2)加速电压U。
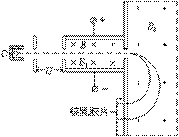 [解析](1)粒子通过速度选择器, 根据匀速运动的
[解析](1)粒子通过速度选择器, 根据匀速运动的
条件: 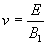 。若测出粒子在偏转磁场的轨道直径为
。若测出粒子在偏转磁场的轨道直径为
d, 则 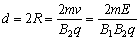 , 所以同位素的荷质比和质量分别为
, 所以同位素的荷质比和质量分别为 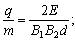 。(2)
。(2)
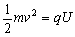 可求得U
可求得U
[专题训练与高考预测]
2、解题思路及方法
圆运动的圆心的确定:
(1)利用洛仑兹力的方向永远指向圆心的特点,只要找到圆运动两个点上的洛仑兹力的方向,其延长线的交点必为圆心.
(2)利用圆上弦的中垂线必过圆心的特点找圆心
1、带电粒子在匀强磁场中运动规律
初速度的特点与运动规律
(1)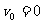
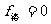 为静止状态
为静止状态
(2)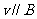
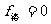 则粒子做匀速直线运动
则粒子做匀速直线运动
(3)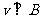
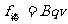 ,则粒子做匀速圆周运动,其基本公式为:
,则粒子做匀速圆周运动,其基本公式为:
向心力公式: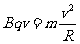
运动轨道半径公式: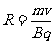 ;
;
运动周期公式: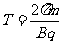
动能公式: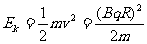
T或 、
、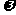 的两个特点:
的两个特点:
T、 和
和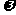 的大小与轨道半径(R)和运行速率(
的大小与轨道半径(R)和运行速率(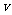 )无关,只与磁场的磁感应强度(B)和粒子的荷质比(
)无关,只与磁场的磁感应强度(B)和粒子的荷质比(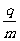 )有关。
)有关。
荷质比(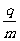 )相同的带电粒子,在同样的匀强磁场中,
)相同的带电粒子,在同样的匀强磁场中,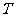 、
、 和
和 相同。
相同。
4、洛伦兹力不做功.
3、洛伦兹力的方向:洛伦兹力方向用左手定则判断
2、洛伦兹力大小:当电荷运动方向与磁场方向平行时,洛伦兹力为零;当电荷运动方向与磁场方向垂直时,洛伦兹力最大,等于qυB;
1、产生洛伦兹力的条件:
(1)电荷对磁场有相对运动.磁场对与其相对静止的电荷不会产生洛伦兹力作用.
(2)电荷的运动速度方向与磁场方向不平行.
15.质量为m、带电量为-q的粒子(重力不计),在匀强电场中A点的瞬时速度为v,方向与电场线垂直,在B点的速度为2v,如图所示。已知A、B两点间的距离为d,求:(1)A、B两点的电势差。(2)电场强度的大小和方向。
14.如图所示,M、N是水平放置的一对金属板,其中M板中央有一个小孔O,板间存在竖直向上的匀强电场.AB是一长9L的轻质绝缘细杆,在杆上等间距地固定着10个完全相同的带正电小球,每个小球的电荷量为q、质量为m,相邻小球距离为L.现将最下端小球置于O处,然后将AB由静止释放,AB在运动过程中始终保持竖直.经观察发现,在第4个小球进入电场到第5个小球进入电场这一过程中AB做匀速运动。求:
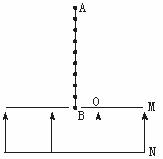 (1)两板间电场强度E;
(1)两板间电场强度E;
(2)上述匀速运动过程中速度v的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com