
1.(安丘市2008年中考化学试题)
某同学在配制50g溶质量分数为5%的食盐溶液的实验中,称量时将砝码放在左盘(1g以下用游码),食盐放在右盘;量水时仰视液面读数。这样配制的食盐溶液中的质量分数
( )
A.等于5% B.大于5%
C.小于5% D.不能确定
例1.下列说法中不正确的是( )
①溶液都是无色透明、均一、稳定的混合物。②同种溶质的饱和溶液一定比它的不饱和溶液浓。③糖水是溶液,盐水是溶液,混合在一起,既有糖又有盐,就不是溶液了。④在某种溶质的饱和溶液中再加入这种溶质,溶液的质量随之增大。⑤一杯调好的糖水,喝第一口特别甜,越喝越不甜,说明后来喝的糖水要变稀些。⑥把饱和溶液温度升高时,若溶液质量不变,则溶液质量也不变。
A.②④⑤⑥ B.①③④⑤ C.①②③④⑤ D.①②③⑤⑥
[解析]此题是有关溶液、饱和溶液概念的判断。溶液不一定无色,故①错。溶液的饱和与否与温度有关,②没有指明温度也不正确。溶液中的溶质可以是一种也可以是多种,故③ 不对。饱和溶液在同条件下不再溶解同种溶质,故④不正确。溶液是均一的,这只是味觉的迟钝造成的错误,故⑤也不正确。⑥正确。
例2.欲将某温度下接近饱和的硝酸钾溶液变成饱和溶液,不能采取的措施是( )
A.加入硝酸钾晶体 B.蒸发一定量水
C.给溶液加热 D.给溶液降温
[解析]本题关键在于充分理解饱和溶液与不饱和溶液的转化条件。因为硝酸钾的溶解度随温度升高而增大。因此降低溶液温度可达到目的。另外,向溶液中加入硝酸钾晶体或蒸发溶剂亦可达到目的。这三种措施单独使用或同时使用都可以。
例3.下图为A、B两种物质的溶解度曲线。回答下列问题:
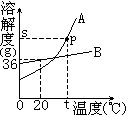 (1)图中P点的含义是____。
(1)图中P点的含义是____。
(2)t℃时,A物质的溶解度___B物质的溶解度(填“大于”、
“小 于”或“等于”)
(3)B物质属于____溶物质(填“易”、“可”、“微”或“难”)
(4)当B中含有少量A时,可用____法提纯B。
[解析]本题主要考查溶解度曲线表示意义,溶解度与溶解性关系
以及结晶法的原理。
例4.某溶液中含有四种离子Na+、Mg2+、Cl-、SO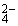 ,其中:Na+、Mg2+、Cl-离子个数比为4:7:6,若Na+离子个数为4a,则SO
,其中:Na+、Mg2+、Cl-离子个数比为4:7:6,若Na+离子个数为4a,则SO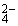 离子个数为____。
离子个数为____。
[解析]解决此类问题的关键是充分理解溶液中电荷守恒原理:所有阳离子带的正电荷总数等于所有阴离子带的负电荷总数。依题意可知:溶液中Mg2+、Cl-的个数分别为7a、6a个。设此时溶液SO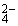 离子数为x,则4a×1+7a×2=6a×1+2x,x=6a。
离子数为x,则4a×1+7a×2=6a×1+2x,x=6a。
6.(人教A版,必修2,P87,B组第1题)
如图5,边长为2的正方形ABCD中,
(1)点 是
是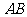 的中点,点
的中点,点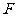 是
是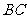 的中点,将
的中点,将 分别沿
分别沿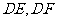 折起,使
折起,使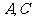 两点重合于点
两点重合于点 ,求证:
,求证: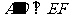 .
.
(2)当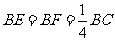 时,求三棱锥
时,求三棱锥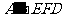 的体积.
的体积.
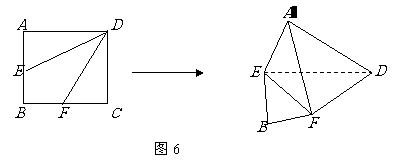

变式题.如图5-1,在矩形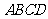 中,
中,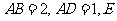 是
是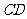 的中点,以
的中点,以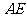 为折痕将
为折痕将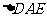 向上折起,使
向上折起,使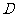 为
为 ,且平面
,且平面 平面
平面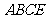 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求直线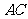 与平面
与平面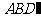 所成角的正弦值.
所成角的正弦值.
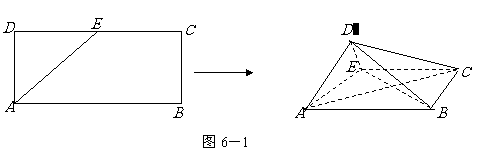

解(Ⅰ)在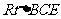 中,
中, ,
,
在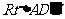 中,
中, ,
,
∵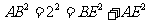 ,
,
∴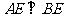 .
.
∵平面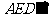 平面
平面 ,且交线为
,且交线为 ,
,
∴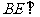 平面
平面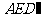 .
.
∵ 平面
平面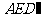 ,
,
∴ .
.
(Ⅱ)设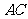 与
与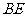 相交于点
相交于点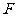 ,由(Ⅰ)知
,由(Ⅰ)知 ,
,
∵ ,
,
∴ 平面
平面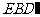 ,
,
∵ 平面
平面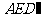 ,
,
∴平面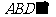 平面
平面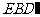 ,且交线为
,且交线为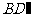 ,
,
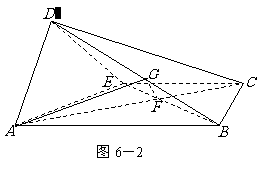
如图6-2,作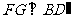 ,垂足为
,垂足为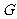 ,则
,则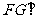 平面
平面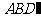 ,
,
连结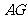 ,则
,则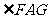 是直线
是直线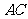 与平面
与平面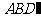 所成的角.
所成的角.
由平面几何的知识可知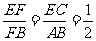 ,∴
,∴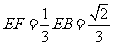 .
.
在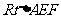 中,
中,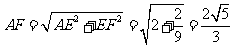 ,
,
在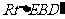 中,
中,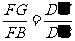 ,可求得
,可求得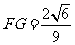 .
.
∴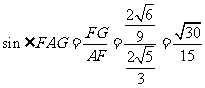 .
.
∴直线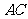 与平面
与平面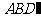 所成的角的正弦值为
所成的角的正弦值为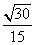 .
.
5.(人教A版,必修2,P87,第10题)
如图5,已知平面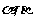 ,且
,且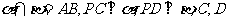 是垂足,试判断直线
是垂足,试判断直线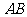 与
与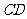 的位置关系?并证明你的结论.
的位置关系?并证明你的结论.
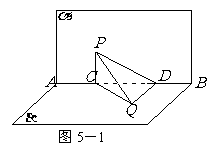 变式题5-1,如图5,已知平面
变式题5-1,如图5,已知平面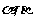 ,且
,且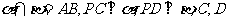 是垂足.
是垂足.
(Ⅰ)求证: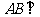 平面
平面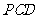 ;
;
(Ⅱ)若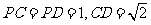 ,试判断平面
,试判断平面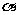 与平面
与平面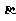 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
变式题5-1,如图5,已知平面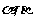 ,
,
且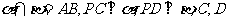 是垂足.
是垂足.
(Ⅰ)求证: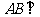 平面
平面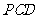 ;
;
(Ⅱ)若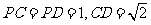 ,试判断平面
,试判断平面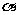 与平面
与平面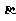 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
解(Ⅰ)因为 ,所以
,所以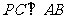 .同理
.同理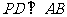 .
.
又 ,故
,故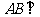 平面
平面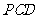 .
.
(Ⅱ)设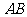 与平面
与平面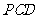 的交点为
的交点为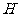 ,连结
,连结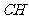 、
、 .
.
因为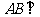 平面
平面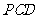 ,所以
,所以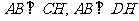 ,
,
所以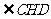 是二面角
是二面角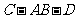 的平面角.
的平面角.
又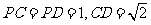 ,所以
,所以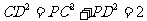 ,即
,即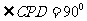 .
.
在平面四边形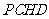 中,
中,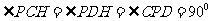 ,
,
所以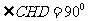 .
.
故平面 平面
平面 .
.
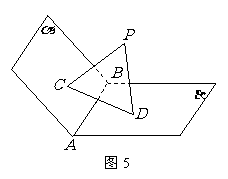
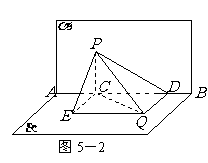 变式题5-2.如图5-1,已知直二面角
变式题5-2.如图5-1,已知直二面角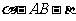 ,
,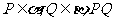 与平面
与平面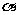 、
、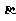 所成的角都为
所成的角都为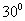 ,
,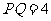 .
.
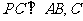 为垂足,
为垂足, 为垂足.
为垂足.
(Ⅰ)求直线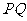 与
与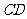 所成角的大小;
所成角的大小;
(Ⅱ)求四面体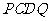 的体积.
的体积.
解:(Ⅰ)如图5-2,在平面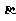 内,作
内,作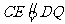 ,连结
,连结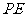 、
、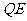 .则四边形
.则四边形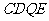 为平行四边形,所以
为平行四边形,所以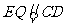 ,即
,即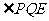 为直线
为直线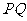 与
与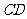 所成的角(或其补角).
所成的角(或其补角).
因为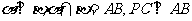 .
.
所以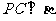 .同理
.同理 .
.
又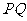 与平面
与平面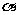 、
、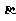 所成角为
所成角为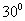 ,所以
,所以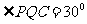 ,
,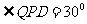 ,所以
,所以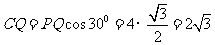 ,
,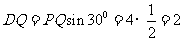 .
.
在 中,
中,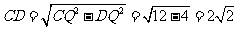 ,从而
,从而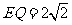 .
.
因为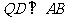 ,且
,且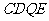 为平行四边形,
为平行四边形,
所以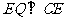 .
.
又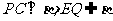 ,所以
,所以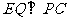 .
.
故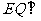 平面
平面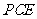 ,从而
,从而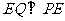 .
.
在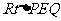 中,
中,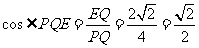 .
.
所以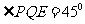 ,
,
即直线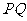 与
与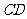 所成角的大小为
所成角的大小为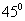 .
.
(Ⅱ)在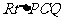 中,
中,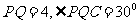 ,所以
,所以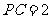 .
.
三角形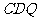 的面积
的面积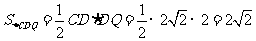 ,
,
故四面体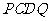 的体积
的体积
 .
.
4.(人教A版,必修2,P74.例2)
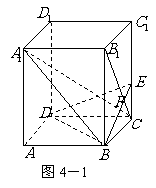
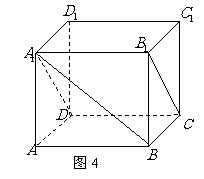 如图4,在正方体
如图4,在正方体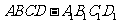 中,求直线
中,求直线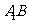 与平面
与平面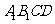 所成的角.
所成的角.
 变式题:如图4-1,已知正四棱柱
变式题:如图4-1,已知正四棱柱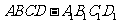 中,底面边长
中,底面边长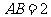 ,侧棱
,侧棱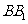 的长为4,过点
的长为4,过点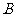 作
作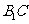 的的垂线交侧棱
的的垂线交侧棱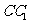 于点
于点 ,交
,交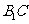 于点
于点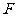 .
.
(Ⅰ)求证: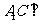 平面
平面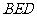 ;
;
(Ⅱ)求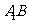 与平面
与平面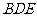 所成的角的正弦值.
所成的角的正弦值.
解:(Ⅰ)如图4-2,以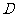 为原点,
为原点,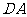 、
、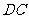 、
、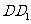 所在直线分别为
所在直线分别为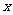 、
、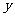 、
、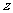 轴建立空间直角坐标系
轴建立空间直角坐标系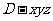 .
.
∴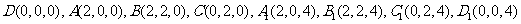 .
.
设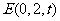 ,则
,则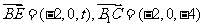 .
.
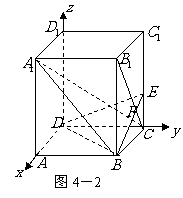 ∵
∵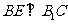 ,∴
,∴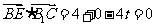 .
.
∴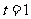 ,∴
,∴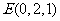 ,
,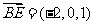 .
.
又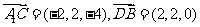 ,
,
∴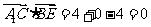 且
且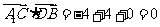 .
.
∴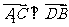 且
且 .
.
∴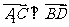 且
且 .∴
.∴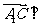 平面
平面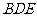 .
.
(Ⅱ)由(Ⅰ)知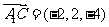 是平面
是平面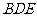 的一个法向量,又
的一个法向量,又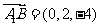 ,
,
∴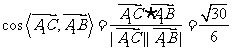 .
.
∴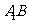 与平面
与平面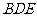 所成角的正弦值为
所成角的正弦值为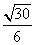 .
.
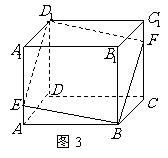
3.(北师大版.必修2.P31.第4题)
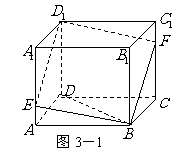
如图3,已知E,F分别是正方体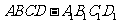 的棱
的棱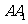 和棱
和棱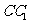 上的点,且
上的点,且 ,求证:四边形
,求证:四边形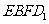 是平行四边形
是平行四边形

变式题:如图3-1.已知 、
、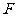 分别是正方体
分别是正方体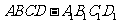 的棱
的棱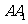 和棱
和棱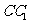 的中点.
的中点.
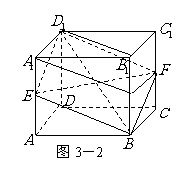 (Ⅰ)试判断四边形
(Ⅰ)试判断四边形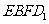 的形状;
的形状;
(Ⅱ)求证:平面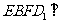 平面
平面 .
.
解(Ⅰ)如图3-2,取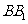 的中点
的中点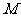 ,连结
,连结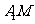 、
、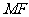 .
.
∵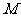 、
、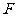 分别是
分别是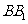 和
和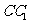 的中点,
的中点,
 ∴
∴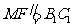 ,
,
在正方体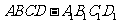 中,有
中,有
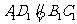 , ∴
, ∴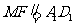 ,
,
∴四边形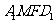 是平行四边形,
是平行四边形,
∴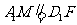 .
.
又 、
、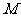 分别是
分别是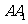 、
、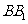 的中点,
的中点,
∴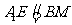 ,
,
∴四边形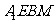 为平行四边形,
为平行四边形,
∴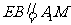 .
.
故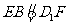 .
.
∴四边形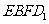 是平行四边形.
是平行四边形.
又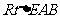 ≌
≌ ,
,
∴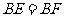 ,
,
故四边形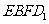 为菱形.
为菱形.
(Ⅱ)连结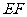 、
、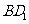 、
、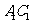 . ∵四边形
. ∵四边形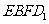 为菱形,
为菱形,
∴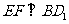 .
.
在正方体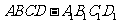 中,有
中,有
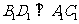 ,
,
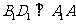
∴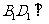 平面
平面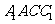 .
.
又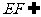 平面
平面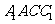 ,
,
∴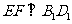 .
.
又 ,
,
∴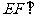 平面
平面 .
.
又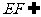 平面
平面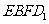 ,
,
故平面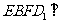 平面
平面
2.(人教A版,必修2,P20.例3)
如图2,已知几何体的三视图,用斜二测画法画出它的直观图.
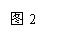
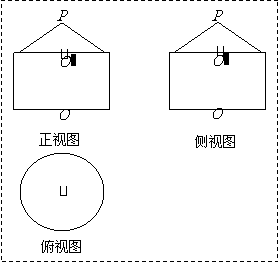
变式题2-1.如图2-1.已知几何体的三视图(单位:cm).
(Ⅰ)画出它的直观图(不要求写画法);
(Ⅱ)求这个几何体的表面积和体积.
|
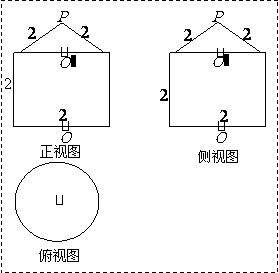
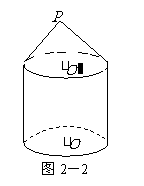
解(Ⅰ)这个几何体的直观图如图2-2所示.
(Ⅱ)这个几何体是一个简单组合体,它的下部是一个圆柱(底面半径为1cm,高为2cm),它的上部是一个圆锥(底面半径为1cm,母线长为2cm,高为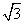 cm).
cm).
所以所求表面积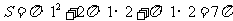
 ,
,
 所求体积
所求体积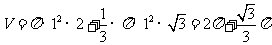
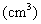 .
.
变式题2-2.如图2-3,已知几何体的三视图(单位:cm).
(Ⅰ)画出这个几何体的直观图(不要求写画法);
(Ⅱ)求这个几何体的表面积及体积;
(Ⅲ)设异面直线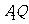 、
、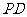 所成角为
所成角为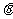 ,求
,求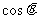 .(理科考生)
.(理科考生)
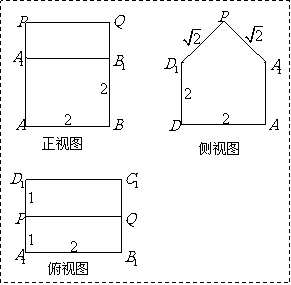

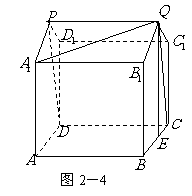
解:(Ⅰ)这个几何体的直观图如图2-4所示.
(Ⅱ)这个几何体可看成是由正方体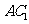 及直三棱柱
及直三棱柱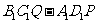 的组合体.
的组合体.
 由
由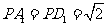 ,
,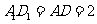 ,
,
可得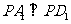 .
.
故所求几何体的全面积
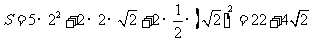
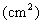
所求几何体的体积
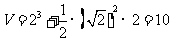
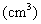
(Ⅲ)由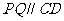 ,且
,且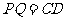 ,可知
,可知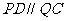 ,
,
故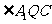 为异面直线
为异面直线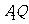 、
、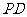 所成的角(或其补角).
所成的角(或其补角).
由题设知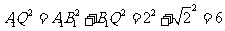 ,
,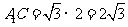 ,
,
取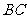 中点
中点 ,则
,则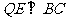 ,且
,且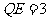 ,
,
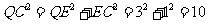 .
.
由余弦定理,得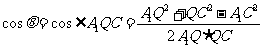
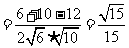 .
.
1.(人教A版,必修2.P17.第4题)
图1是一个几何体的三视图,想象它的几何结构特征,并说出它的名称.


变式题1.如图1-1是一个几何体的三视图(单位:cm)
(Ⅰ)画出这个几何体的直观图(不要求写画法);
(Ⅱ)求这个几何体的表面积及体积;
(Ⅲ)设异面直线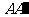 与
与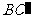 所成的角为
所成的角为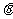 ,求
,求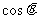 .
.
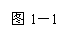
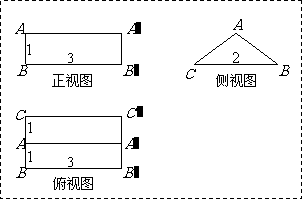
解:(Ⅰ)这个几何体的直观图如图1-2所示.
(Ⅱ)这个几何体是直三棱柱.
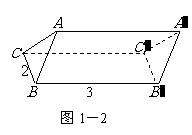 由于底面
由于底面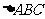 的高为1,所以
的高为1,所以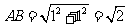 .
.
故所求全面积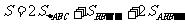

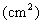 .
.
这个几何体的体积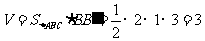
(Ⅲ)因为 ,所以
,所以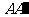 与
与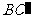 所成的角是
所成的角是 .
.
在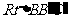 中,
中, ,
,
故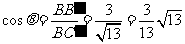 .
.
66. We usually work eight hours ___________.
A. everyday B. one day C. a day D. in a day
Keys:
1-5. DCABA 6-10. BCCAB 11-15. DBBDA 16-20. CDDAD
21-25. ACAAD 26-30. BDDCC 31-35. BCBCB 36-40. DADDC
41-45. AAADC 46-50. BDCBB 51-55. ABBAD 56-60. BAABA
61-66. CDCCAC
65. Great changes __________ last year.
A. took place B. were taken
place C. had
broken out D.
happened
B. were taken
place C. had
broken out D.
happened
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com