
1.下列等式不正确的是
( )
A.a+0=a B.a+b=b+a
C.+≠0 D.=++
[解析] 解法1:∵与为相反向量,
∴+=0,∴C不正确.
解法2:+=(-)+(-)
=--+=0.∴C不正确.
[答案] C
23.(本小题满分10分)
一个袋中装有黑球,白球和红球共n(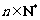 )个,这些球除颜色外完全相同.已知从袋中任意摸出1个球,得到黑球的概率是
)个,这些球除颜色外完全相同.已知从袋中任意摸出1个球,得到黑球的概率是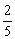 .现从袋中任意摸出2个球.
.现从袋中任意摸出2个球.
(1)若n=15,且摸出的2个球中至少有1个白球的概率是 ,设
,设 表示摸出的2个球中红球的个数,求随机变量
表示摸出的2个球中红球的个数,求随机变量 的概率分布及数学期望
的概率分布及数学期望 ;
;
(2)当n取何值时,摸出的2个球中至少有1个黑球的概率最大,最大概率为多少?
22. (本小题满分10分)
(本小题满分10分)
如图,在直三棱柱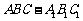 中,
中, ,AB=AC=a,
,AB=AC=a,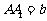 ,点E,F分别在棱
,点E,F分别在棱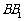 ,
,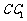 上,且
上,且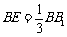 ,
,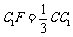 .设
.设 .
.
(1)当 =3时,求异面直线
=3时,求异面直线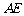 与
与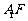 所成角的大小;
所成角的大小;
(2)当平面 ⊥平面
⊥平面 时,求
时,求 的值.
的值.
21.[选做题]在A、B、C、D 四小题中只能选做两题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
A.选修4-1:几何证明选讲
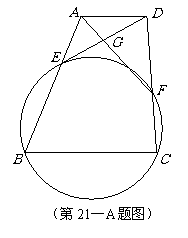 如图,在梯形
如图,在梯形 中,
中, ∥BC,点
∥BC,点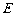 ,
,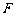 分别在边
分别在边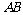 ,
, 上,设
上,设 与
与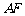 相交于点
相交于点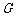 ,若
,若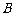 ,
,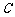 ,
,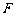 ,
,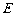 四点共圆,求证:
四点共圆,求证: .
.
B.选修4-2:矩阵与变换
已知矩阵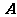 =
=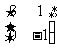 ,求
,求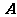 的特征值
的特征值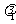 ,
,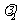 及对应的特征向量
及对应的特征向量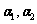 .
.
C.选修4-4:坐标系与参数方程
已知曲线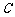 的方程
的方程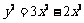 ,设
,设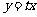 ,
, 为参数,求曲线
为参数,求曲线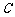 的参数方程.
的参数方程.
D.选修4-5:不等式选讲
设实数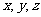 满足
满足 ,求
,求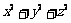 的最小值,并求此时
的最小值,并求此时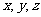 的值.
的值.
[必做题]第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
20. [解]:(1)当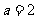 时,
时,
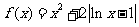
 …………(2分)
…………(2分)
当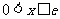 时,
时,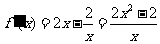 ,
,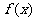 在
在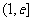 内单调递增;
内单调递增;
当 时,
时, 恒成立,故
恒成立,故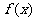 在
在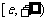 内单调递增;
内单调递增;
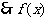 的单调增区间为
的单调增区间为 。
…………(6分)
。
…………(6分)
(2)①当 时,
时,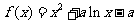 ,
,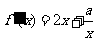
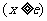
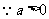 ,
,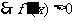 恒成立,
恒成立,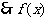 在
在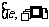 上增函数。
上增函数。
故当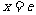 时,
时,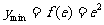 。
…………8分)
。
…………8分)
②当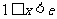 时,
时, ,
,

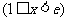
(Ⅰ)当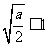 ,即
,即 时,
时,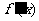 在
在 时为正数,所以
时为正数,所以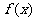 在区间
在区间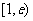 上为增函数。故当
上为增函数。故当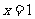 时,
时, ,且此时
,且此时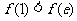 …………(10分)
…………(10分)
(Ⅱ)当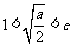 ,即
,即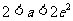 时,
时,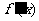 在
在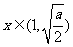 时为负数,在
时为负数,在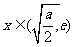 时为正数,所以
时为正数,所以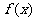 在区间
在区间 上为减函数,在
上为减函数,在 上为增函数。故当
上为增函数。故当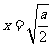 时,
时, ,且此时
,且此时 。
…………(12分)
。
…………(12分)
(Ⅲ)当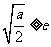 ,即
,即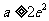 时,
时,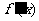 在
在 进为负数,所以
进为负数,所以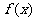 在区间
在区间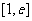 上为减函数,故当
上为减函数,故当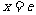 时,
时,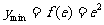 。
…………(14分)
。
…………(14分)
所以函数 的最小值为
的最小值为 。
。
由条件得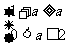 此时
此时 ;或
;或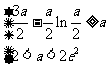 ,此时
,此时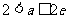 ;或
;或 ,此时无解。
,此时无解。
综上,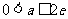 。
…………(16分)
。
…………(16分)
数学Ⅱ(附加题)
20.(本小题满分16分)设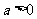 ,函数
,函数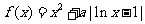 .
.
(Ⅰ)当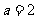 时,求函数
时,求函数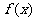 的单调增区间;
的单调增区间;
(Ⅱ)若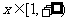 时,不等式
时,不等式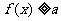 恒成立,实数
恒成立,实数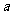 的取值范围..
的取值范围..
19.(本小题满分16分)
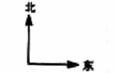 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东
在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东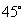 且与点A相距40
且与点A相距40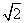 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东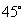 +
+ (其中sin
(其中sin =
=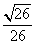 ,
, )且与点A相距10
)且与点A相距10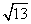 海里的位置C.
海里的位置C.
(1)求该船的行驶速度(单位:海里/时);
(I2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
19解 (1)如图,AB=40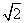 ,AC=10
,AC=10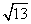 ,
,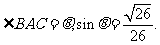
由于0< <
<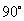 ,所以cos
,所以cos =
=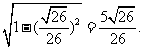 ……………………………2分
……………………………2分
由余弦定理得BC=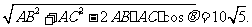 ……………………6分
……………………6分
所以船的行驶速度为 (海里/小时). ……………………………8分
(海里/小时). ……………………………8分
(2)解法一 如图所示,以A为原点建立平面直角坐标系,设点B、C的坐标分别是
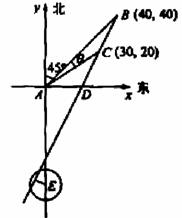 B(x1,y2),
C(x1,y2),BC与x轴的交点为D.
B(x1,y2),
C(x1,y2),BC与x轴的交点为D.
由题设有,x1=y1=

 AB=40, ……10分
AB=40, ……10分
x2=ACcos .
.
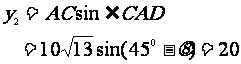 ……12分
……12分
所以过点B、C的直线l的斜率k=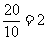 ,直线l的方程为y=2x-40.
,直线l的方程为y=2x-40.
又点E(0,-55)到直线l的距离d=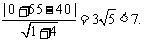 …………15分
…………15分
所以船会进入警戒水域. ……………………………16 分
解法二 如图所示,设直线AE与BC的延长线相交于点Q.在△ABC中,
由余弦定理得,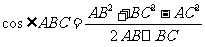
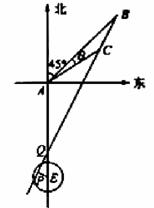 ==
==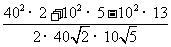 =
=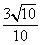 .…………10 分
.…………10 分
从而
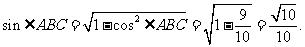
在 中,由正弦定理得,
中,由正弦定理得,
AQ=
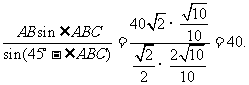 …………12分
…………12分
由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.过点E作EP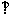 BC于点P,则EP为点E到直线BC的距离.
BC于点P,则EP为点E到直线BC的距离. 在Rt
在Rt 中,
中,
PE=QE·sin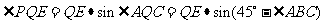
=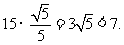 ………………………15 分
………………………15 分
所以船会进入警戒水域. ………………………16 分
18. 解:(1)设点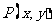 ,依题意,有
,依题意,有
 . ----------2分
. ----------2分
整理,得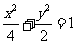 .
.
所以动点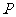 的轨迹
的轨迹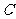 的方程为
的方程为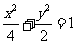 . -------------5分
. -------------5分
(3)由题意:设N ,A
,A 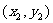 ,则B
,则B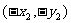
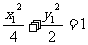 ,
, ---------------7分
---------------7分
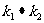 =
=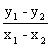
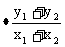 =
=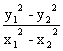
=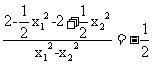 为定值。-----------------------------10分设
为定值。-----------------------------10分设
(2)M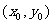 ,则切线MQ的方程为:
,则切线MQ的方程为: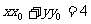
由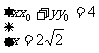 得Q
得Q ------------12分
------------12分
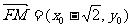 ,
, 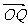
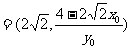

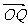 =
=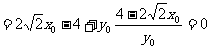 ----------15分
----------15分
所以: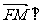
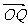 即MF与OQ始终保持垂直关系 -------------16分
即MF与OQ始终保持垂直关系 -------------16分
18.(本小题满分16分)已知动点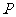 到定直线
到定直线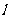 :
: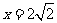 的距离与点
的距离与点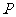 到定点
到定点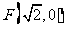 之比为
之比为 .
.
(1)求动点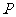 的轨迹
的轨迹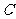 的方程;
的方程;
(2)若点N为轨迹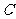 上任意一点(不在x轴上),过原点O作直线AB交(1)中轨迹C于点A、B,且直线AN、BN的斜率都存在,分别为
上任意一点(不在x轴上),过原点O作直线AB交(1)中轨迹C于点A、B,且直线AN、BN的斜率都存在,分别为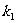 、
、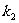 ,问
,问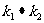 是否为定值?
是否为定值?
(3)若点M为圆O: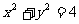 上任意一点(不在x轴上),过M作圆O的切线,交直线
上任意一点(不在x轴上),过M作圆O的切线,交直线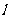 于点Q,问MF与OQ是否始终保持垂直关系?
于点Q,问MF与OQ是否始终保持垂直关系?
17.(本小题满分14分)
已知分别以 和
和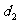 为公差的等差数列
为公差的等差数列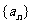 和
和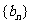 满足
满足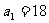 ,
, .
.
(1)若 =18,且存在正整数
=18,且存在正整数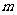 ,使得
,使得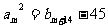 ,求证:
,求证: ;
;
(2)若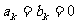 ,且数列
,且数列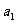 ,
,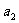 ,…,
,…,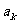 ,
,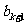 ,
,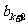 ,…,
,…,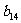 的前
的前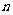 项和
项和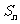 满足
满足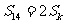 ,求数列
,求数列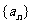 和
和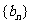 的通项公式;
的通项公式;
17解:(1)依题意,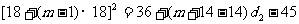 ,
,
即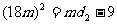 , 即
, 即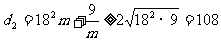 ;………4分
;………4分
等号成立的条件为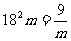 ,即
,即 ,
,
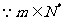 ,
,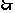 等号不成立,
等号不成立,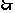 原命题成立. …………………………7分
原命题成立. …………………………7分
(2)由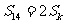 得:
得: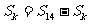 ,即:
,即: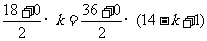 ,
,
则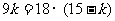 ,得
,得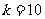 …………………………11分
…………………………11分
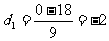 ,
, , …………………………13分
, …………………………13分
则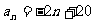 ,
,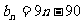 ;
………………………………14分
;
………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com