11．(15分)如图，以向量＝a，＝b为边作▱OADB，＝，＝，用a，b表示、、.

[解析]　∵＝＝＝a－b，

＝＝a－b.

∴＝+＝a+b，又＝a+b，

＝+＝+＝＝(a+b)．

∴＝－＝a+b－a－b＝a－b.

即有＝a+b，＝a+b，＝a－b.

10．(15分)设i、j分别是平面直角坐标系Ox、Oy正方向上的单位向量，且＝－2i+mj，＝ni+j，＝5i－j，若点A、B、C在同一条直线上，且m＝2n，求实数m、n的值．

[解析]　＝－＝(n+2)i+(1－m)j，

＝－＝(5－n)i+(－2)j.

∵点A、B、C在同一条直线上，∴∥，

即＝λ，

∴(n+2)i+(1－m)j＝λ[(5－n)i+(－2)j]，

∴，解得或.

9．(2009年安徽卷)在平行四边形ABCD中，E和F分别是边CD和BC的中点，若＝λ+μ，其中λ、μ∈R，则λ+μ＝________.

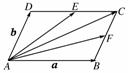
[解析]　设＝a，＝b，

那么＝a+b，

＝a+b.

又∵＝a+b.

∴＝(+)，即λ＝μ＝，∴λ+μ＝.

[答案]　

8．已知平面上不共线的四点O，A，B，C.若－3+2＝0，则等于________．

[解析]　由已知得：(－)+2(－)＝+2＝0⇒＝2，根据数乘的意义可得：＝2⇒＝2.

[答案]　2

7．已知四边形ABCD中，＝，且||＝||，则四边形ABCD的形状是________．

[解析]　＝⇒∥，且||＝||，

∴ABCD为梯形，又||＝||，∴为等腰梯形．

[答案]　等腰梯形

6．已知向量a、b、c中任意两个都不共线，并且a+b与c共线，b+c与a共线，那么a+b+c等于

(　)

A．a　 　　　　　　　　　　　　　　　 B．b

C．c　 　　　　　　　　　　　　　　　 D．0

[解析]　∵a+b与c共线，

∴a+b＝λ₁c①

又∵b+c与a共线，∴b+c＝λ₂a②

由①得：b＝λ₁c－a.

∴b+c＝λ₁c－a+c＝(λ₁+1)c－a＝λ₂a，

∴即，

∴a+b+c＝－c+c＝0.

[答案]　D

5．已知平面内有一点P及一个△ABC，若++＝，则

(　)

A．点P在△ABC外部　 　　 B．点P在线段AB上

C．点P在线段BC上　 　　　 D．点P在线段AC上

[解析]　∵++＝，

∴++－＝0，

即+++＝0，

∴++＝0，

2＝，∴点P在线段AC上．

[答案]　D

4．设＝x+y，且A、B、C三点共线(该直线不过端点O)，则x+y等于

(　)

A．1　 　　　　　 　　　　　　　　　　 B．－1

C．0　 　　　　　　　　　　　　　　　 D．不能确定

[解析]　∵A、B、C三点共线，

∴存在一个实数λ，使＝λ，

即－＝λ(－)．

∴＝(1－λ)+λ.

又∵＝x+y，

∴x+y＝(1－λ)+λ＝1.

[答案]　A

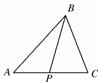
3．(2009年山东卷)设P是△ABC所在平面内的一点，+＝2，则

(　)

A.+＝0　 　　　　　　　　　 B.+＝0

C.+＝0　 　　　　　　　　　 D.++＝0

[解析]　因为+＝2，

所以点P为线段AC的中点，故选B.

[答案]　B

2．在四边形ABCD中，＝a+2b，＝－4a－b，＝－5a－3b，则四边形ABCD的形状是

(　)

A．矩形　 　　　　　　　　　　　　　 B．平行四边形

C．梯形　 　　　　　　　　　　　　　 D．以上都不对

[解析]　由已知＝++＝－8a－2b＝2(－4a－b)＝2.

∴∥，又与不平行，

∴四边形ABCD是梯形．

[答案]　C