
1.设集合A={1,2,3,4},B={0,1,2,4,5},全集U=A∪B,则集合∁U (A∩B)中的元素共有 ____________ 个.
2 已知
已知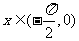 ,
,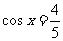 ,则
,则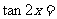 ________________.
________________.
3 在△ABC中,
在△ABC中,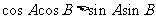 ,则△ABC为________________三角形.
,则△ABC为________________三角形.
2.已知下列不等式,比较正数m、n的大小:
(1)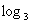 m<
m<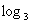 n
(2)
n
(2) 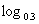 m>
m>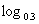 n
n
(3) 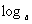 m<
m<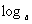 n(0<a<1) (4)
n(0<a<1) (4)
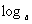 m>
m>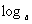 n(a>1)
n(a>1)

解:(1)考查函数y=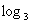 x
x
∵3>1,∴函数y=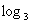 x在(0,+∞)是增函数
x在(0,+∞)是增函数
∵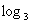 m<
m<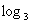 n,∴m<n
n,∴m<n
(2)考查函数y=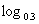 x
x
∵0<0.3<1,∴函数y=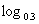 x在(0,+∞)上是减函数
x在(0,+∞)上是减函数
∵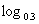 m>
m>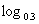 n,
n,
∴m<n
(3)考查函数y=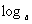 x
x
∵0<a<1,
∴函数y=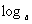 x在(0,+∞)上是减函数
x在(0,+∞)上是减函数
∵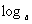 m<
m<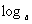 n,
n,
∴m>n
(4)考查函数y=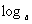 x
x
∵a>1,
∴函数y=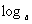 x在(0,+∞)上是增函数
x在(0,+∞)上是增函数
∵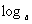 m>
m>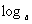 n,
n,
∴m>n
1.比较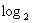 0.7与
0.7与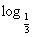 0.8两值大小
0.8两值大小
解:考查函数y=log2x
∵2>1,∴函数y=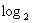 x在(0,+∞)上是增函数
x在(0,+∞)上是增函数
又0.7<1,∴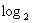 0.7<
0.7<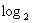 1=0
1=0
再考查函数y=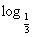 x
x
∵0<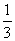 <1
<1
∴函数y=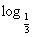 x在(0,+∞)上是减函数
x在(0,+∞)上是减函数
又1>0.8,∴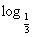 0.8>
0.8>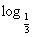 1=0
1=0
∴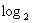 0.7<0<
0.7<0<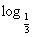 0.8
0.8
∴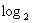 0.7<
0.7<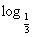 0.8
0.8
比较对数大小的方法,两种情况,求函数定义值域的方法
⑴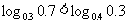

⑵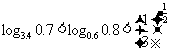

⑶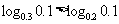

例1比较下列各组数中两个值的大小:
⑴ ;
⑵
;
⑵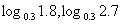 ;
;
⑶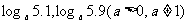

解:⑴考查对数函数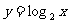 ,因为它的底数2>1,所以它在(0,+∞)上是增函数,于是
,因为它的底数2>1,所以它在(0,+∞)上是增函数,于是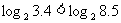

⑵考查对数函数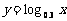 ,因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是
,因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是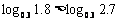

小结1:两个同底数的对数比较大小的一般步骤:
①确定所要考查的对数函数;
②根据对数底数判断对数函数增减性;
③比较真数大小,然后利用对数函数的增减性判断两对数值的大小
⑶当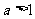 时,
时,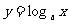 在(0,+∞)上是增函数,于是
在(0,+∞)上是增函数,于是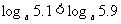
当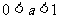 时,
时,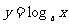 在(0,+∞)上是减函数,于是
在(0,+∞)上是减函数,于是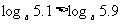
小结2:分类讨论的思想
对数函数的单调性取决于对数的底数是大于1还是小于1 而已知条件并未指明,因此需要对底数
而已知条件并未指明,因此需要对底数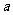 进行讨论,体现了分类讨论的思想,要求学生逐步掌握
进行讨论,体现了分类讨论的思想,要求学生逐步掌握
例3比较下列各组中两个值的大小:
⑴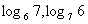 ;
⑵
;
⑵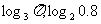

分析:由于两个对数值不同底,故不能直接比较大小,可在两对数值中间插入一个已知数,间接比较两对数的大小
解:⑴ ,
,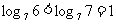 ,
,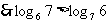

⑵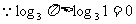 ,
,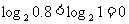 ,
, ;
;
小结3:引入中间变量比较大小
例3仍是利用对数函数的增减性比较两个对数的大小,当不能直接比较时,经常在两个对数中间插入1或0等,间接比较两个对数的大小
例4 求下列函数的定义域、值域:
⑴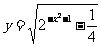 ⑵
⑵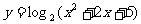
⑶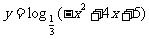 ⑷
⑷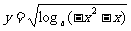
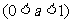

解:⑴要使函数有意义,则须:
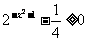 即:
即: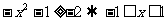
∵ ∴
∴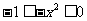 从而
从而 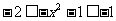
∴ ∴
∴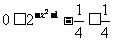 ∴
∴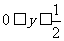
∴定义域为[-1,1],值域为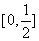

⑵∵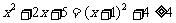 对一切实数都恒成立
对一切实数都恒成立
∴函数定义域为R
从而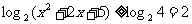 即函数值域为
即函数值域为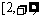

⑶要使函数有意义,则须:

由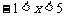 ∴在此区间内
∴在此区间内
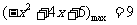
∴ 

从而 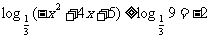 即:值域为
即:值域为
∴定义域为[-1,5],值域为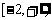

⑷要使函数有意义,则须: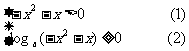
由①: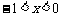
由②:∵ 时 则须
时 则须 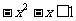 ,
,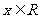
综合①②得 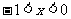

当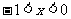 时
时 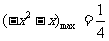 ∴
∴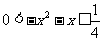
∴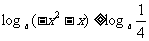 ∴
∴ 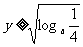
∴定义域为(-1,0),值域为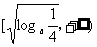

2、对数函数的性质:
|
|
a>1 |
0<a<1 |
|
图 象 |
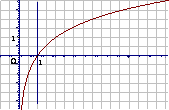 |
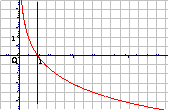 |
|
性 质 |
定义域:(0,+∞) |
|
值域:R |
||
过点(1,0),即当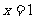 时, 时,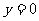  |
||
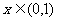 时 时 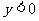  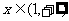 时 时 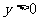  |
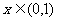 时 时 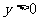  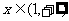 时 时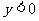  |
|
在(0,+∞)上是增函数 |
在(0,+∞)上是减函数 |
1、指对数互化关系::

Dear Jim,
 I’m really looking forward to your coming
here and I’m sure you will be deeply impressed by a new Shanghai.
I’m really looking forward to your coming
here and I’m sure you will be deeply impressed by a new Shanghai.
Best wishes,
Yours.
 Li
Hua
Li
Hua
第二节 书面表达(满分25分)
加入你是李华,你的美国笔友Jim 计划要到中国上海观光并参观世博园。 请你根据下列表格中的信息,在信中向他介绍一下上海。
|
面积 |
7037.50平方千米 |
|
人口 |
超过1800万 |
|
名胜 |
东方明珠,豫园等 |
|
交通 |
公共汽车,出租车,地铁等 |
|
世博园 |
5个场馆群(各国,国际组织等博览会展示馆);世博会定于2010年5月1日至10月31日举行 |
注意:
1.100词左右。
2.开头和结尾处已给出,不计入总词数。
3.信中内容必须包括表格所提供的要点(可适当增加内容)
4.参考词汇: the Oriental Pearl Tower 东方明珠 Yu Garden 豫园
Pavilion(展览会的)展示馆
Expo 2010 Shanghai 上海世博会
上海世博会
Dear Jim,
Learing that you are coming to visit Shanghai and the Expo Garden, I’m very glad to offer you some information about the city.
_______________________________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Best wishes,
Yours,
Li Hua
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com