
23. ---He suggests the number of cars should be limited to stop air pollution.
--- __________, the idea is not very practical.
A. Sounds good as it B. As it sounds good
C. As good it sounds D. Good as it sounds
22. Scientists are trying to develop a special material, _______ they will make use of in space.
A. it B. that C. what D. one
第一节:单项填空:(共15小题;每小题1分,满分15分)
21. The education of _______young is always _______ hot and serious topic in modern society.
A. the; / B. a; the C. /; the D. the; a
4.已知非零实数a、b满足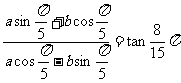 ,求
,求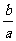 的值
的值
解法一:所给等式左边的分子、分母同除以a,则已知等式化为关于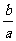 的方程,可求出
的方程,可求出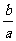

解:由题设得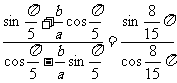
解这个关于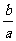 的方程得
的方程得
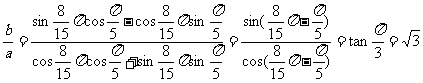

解法二:已知等式的左边的分子、分母都具有asinα+bcosα的结构,可考虑引入辅助角求解
解:∵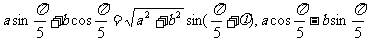
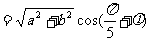

其中 ,即
,即

∴由题设得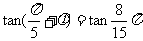
故 ,即
,即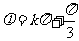 (k∈Z)
(k∈Z)
因此,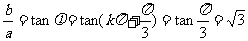

解法三:在已知等式的左边,分子与分母同时除以acos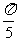 得:
得: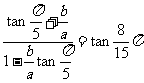

令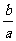 =tanθ,则
=tanθ,则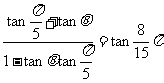
∴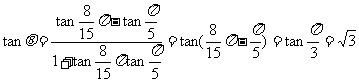

评注:解法一利用了集中变量的思想,是一种基本方法 解法二通过模式联想,引入辅助角,解法三通过联想两角和的正切公式,利用了换元法,实质上是综合了解法一和解法二的优点
解法二通过模式联想,引入辅助角,解法三通过联想两角和的正切公式,利用了换元法,实质上是综合了解法一和解法二的优点
2.已知α、β、γ组成公差为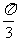 的等差数列,求tanα·tanβ+tanβtanγ+tanγtanα的值
的等差数列,求tanα·tanβ+tanβtanγ+tanγtanα的值
分析:条件的使用形式较多,可以把α、β、γ通过条件置换成β=α=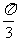 ,γ=α+
,γ=α+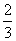 π;也可以用等差中项公式β=
π;也可以用等差中项公式β=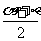 ,但两种形式置换后的结果比较复杂
,但两种形式置换后的结果比较复杂 化切为弦虽是一种常用方法,但在这里效果不明显
化切为弦虽是一种常用方法,但在这里效果不明显 如果换个角度使用条件,即把条件变为β-α=
如果换个角度使用条件,即把条件变为β-α=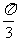 ,γ-β=
,γ-β=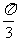 ,γ-α=
,γ-α=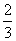 π,两边取正切后可分别出现所求式中的tanαtanβ、tanβtanγ、tanγtanα,然后将它们整体代入,便可使问题解决
π,两边取正切后可分别出现所求式中的tanαtanβ、tanβtanγ、tanγtanα,然后将它们整体代入,便可使问题解决
解:由条件得β-α=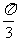 ,两边取正切得tan (β-α)=tan
,两边取正切得tan (β-α)=tan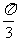 ,即
,即 ,化简可得tanαtanβ=
,化简可得tanαtanβ= (tanβ-tanα)-1
①
(tanβ-tanα)-1
①
同理,由γ-β=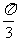 得tanγtanβ=
得tanγtanβ= (tanγ-tanβ)-1
②
(tanγ-tanβ)-1
②
由γ-α=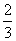 π得tanγtanα=
π得tanγtanα= (tanα-tanγ)-1
③
(tanα-tanγ)-1
③
以上三式相加得tanαtanβ+tanβtanγ+tanγtanα=-3
1.求证: =32cos20°
=32cos20°
分析:本题证明方向显然是从左边证到右边 同时,注意到角与函数次数的变化,运用降幂公式sin2α=
同时,注意到角与函数次数的变化,运用降幂公式sin2α= 可使等式中的角与函数的次数得到统一
可使等式中的角与函数的次数得到统一
证法一:左边=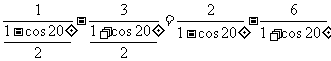
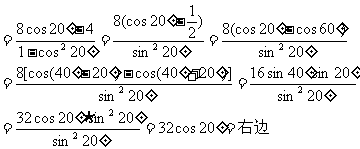
∴原式成立
证法二:左边=
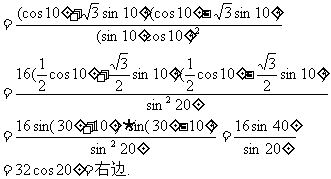
∴原式成立
评注:关于三角函数的化简、求值、证明问题要善于观察、联想公式之间的内在联系,通过拆、配等方法去分析问题和解决问题 证法一中的常值代换(
证法一中的常值代换(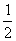 用cos60°代),角的分拆(20°分成40°-20°,60°分成40°+20°)及公式的逆用,是实施三角变形的重要方法
用cos60°代),角的分拆(20°分成40°-20°,60°分成40°+20°)及公式的逆用,是实施三角变形的重要方法
例1在△ABC中,已知cosA =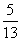 ,sinB =
,sinB =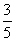 ,则cosC的值为…………(A)
,则cosC的值为…………(A)
A
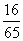 B
B
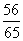 C
C
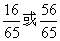 D
D
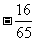
解:∵C = p - (A + B) ∴cosC = - cos(A + B)
又∵AÎ(0, p) ∴sinA =  而sinB =
而sinB =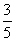 显然sinA > sinB
显然sinA > sinB
∴A
> B 即B必为锐角 ∴ cosB = 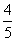
∴cosC
= - cos(A + B) = sinAsinB -
cosAcosB =
例2在△ABC中,ÐC>90°,则tanAtanB与1的关系适合………………(B)
A tanAtanB>1 B
tanAtanB>1 B tanAtanB>1 C
tanAtanB>1 C tanAtanB =1 D
tanAtanB =1 D 不确定
不确定
解:在△ABC中 ∵ÐC>90° ∴A, B为锐角 即tanA>0, tanB>0
又:tanC<0 于是:tanC
= -tan(A+B) =  <0
<0
∴1 - tanAtanB>0 即:tanAtanB<1
又解:在△ABC中 ∵ÐC>90° ∴C必在以AB为直径的⊙O内(如图)

|
设CD = h,C’D = h’,AD = p,BD = q,
|
|
|

例3已知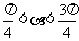 ,
,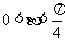 ,
,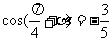 ,
,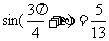 ,
,
求sin(a + b)的值
解:∵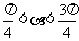 ∴
∴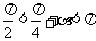
又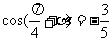 ∴
∴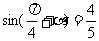
∵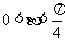 ∴
∴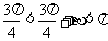
又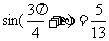 ∴
∴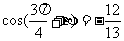
∴sin(a + b) = -sin[p + (a + b)] = 
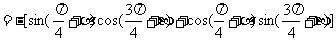
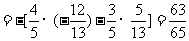
例4已知sina +
sinb = 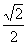 ,求cosa + cosb的范围
,求cosa + cosb的范围
解:设cosa + cosb = t,
则(sina +
sinb)2 + (cosa + cosb)2 = 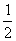 + t2
+ t2
∴2
+ 2cos(a - b) = 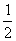 + t2
+ t2
即
cos(a - b) = 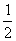 t2 -
t2 -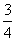
又∵-1≤cos(a - b)≤1 ∴-1≤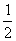 t2 -
t2 -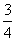 ≤1
≤1
∴ ≤t≤
≤t≤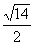
例5设a,bÎ(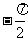 ,
,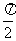 ),tana、tanb是一元二次方程
),tana、tanb是一元二次方程 的两个根,求 a + b
的两个根,求 a + b
解:由韦达定理: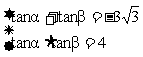
∴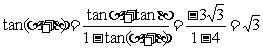
又由a,bÎ(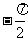 ,
,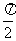 )且tana,tanb < 0 (∵tana+tanb<0,
tanatanb >0)
)且tana,tanb < 0 (∵tana+tanb<0,
tanatanb >0)
得a + bÎ (-p, 0) ∴a + b = 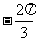
例6 已知sin(p - a) - cos(p + a) =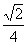 (0<a<p),求sin(p + a) + cos(2p - a)的值
(0<a<p),求sin(p + a) + cos(2p - a)的值
解:∵sin(p - a) - cos(p + a) =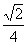 即:sin a + cos a =
即:sin a + cos a =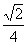 ①
①
又∵0<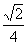 <1,0<a<p
<1,0<a<p  ∴sina>0, cosa<0
∴sina>0, cosa<0
令a = sin(p + a) + cos(2p - a) = - sina + cosa 则 a<0
由①得:2sinacosa = 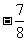
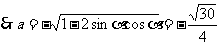
例7 已知2sin(p - a) - cos(p + a) = 1 (0<a<p),求cos(2p - a) + sin(p + a)的值
解:将已知条件化简得:2sin a + cos a = 1 ①
设cos(2p - a) + sin(p + a) = a , 则 a = cos a - sin a ②
①②联立得: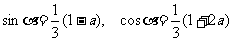
∵sin2a + cos2a =
1 ∴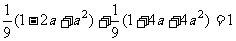
∴5a2 + 2a - 7 = 0,
解之得:a1 = 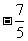 , a2 = 1(舍去)(否则sina = 0,
与0<a<p不符)
, a2 = 1(舍去)(否则sina = 0,
与0<a<p不符)
∴cos(2p - a) + sin(p + a) = 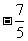
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com