12．(16分)某商品在近30天内每件的销售价格P(元)与时间t(天)的函数是：

P＝

该商品的日销售量Q(件)与时间t(天 )的函数关系是：

Q＝－t+40(0＜t≤30，t∈N₊)，求这种商品的日销售金额的最大值．

[解析]　设日销售金额为y元，则y＝P·Q

y＝

当0＜t＜25，t∈N₊时，

y＝－t²+20t+800＝－(t－10)²+900，

∴t＝10时，y_max＝900元．

当25≤t≤30，t∈N₊时，

y＝t²－140t+4 000＝(t－70)²－900，

∴t＝25时，y_max＝1125元．

综上所述，这种商品日销售额的最大值为1125元.

11．(15分)已知函数y＝的定义域为R.

(1)求实数m的取值范围；

(2)当m变化时，若y的最小值为f(m)，求函数f(m)的值域．

[解析]　(1)依题意，当x∈R时，mx²－6mx+m+8≥0恒成立．当m＝0时，x∈R；

当m≠0时，

即

解之得0＜m≤1，故0≤m≤1.

(2)当m＝0时，y＝2；

当0＜m≤1，y＝.

∴y_min＝.

因此，f(m)＝(0≤m≤1)．

∴f(m)的值域为[0,2]．

10．(15分)求下列函数的定义域：

(1)y＝+；

(2)已知函数f(2x+1)的定义域为(0,1)，求f(x)的定义域．

[解析]　(1)要使函数有意义，

应有即有

所以函数的定义域是{x|－1≤x＜1，或1＜x＜2}．

(2)∵f(2x+1)的定义域为(0,1)，∴1＜2x+1＜3，

所以f(x)的定义域是(1,3)．

9．已知函数y＝f(x)的定义域是[0,2]，那么g(x)＝的定义域是________．

[解析]　由

∴－≤x≤且x≠－1.

[答案]　[－，－1)∪(－1，]

8．函数y＝f(x)的图象如图所示．那么，f(x)的定义域是____；值域是________；

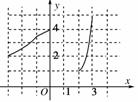
其中只与x的一个值对应的y值的范围是　　.

[解析]　由图象知，函数y=f(x)的图象包括两部分，一部分是以点(-3,2)和(0,4)为两个端点的一条曲线段，一部分是以(2,1)为起点到(3,5)结束的曲线段，故其定义域是[-3,0]∪[2,3]，值域为[1,5]，只与x的一个值对应的y值的取值范围是[1,2)∪(4,5]．

[答案]　[-3,0]∪[2,3]　[1,5]　[1,2)∪(4,5]

7．函数y＝+ 的定义域是________．

[解析]　⇒⇒x≤－1.

[答案]　(－∞，－1]

6．若函数f(x)＝(a²－2a－3)x²+(a－3)x+1的定义域和值域都为R，则a的取值范围是(　)

A．a＝－1或a＝3　 　　B．a＝－1

C．a＝3　 　　　　　　D．a不存在

[解析]　依题意应有，解得a＝－1.

[答案]　B

5．定义运算：a*b＝如1](　)

A．R　 　　　　B．(0，+∞)

C．(0,1]　 　　　D．[1，+∞)

[解析]　f(x)＝

∴0＜f(x)≤1，故选C.

[答案]　C

4．函数f(x)＝+2^lg(1－x)的定义域是(　)

A. 　　　B.

C. 　　　　D.

[解析]　由得－＜x＜1，即函数的定义域是，选B.

[答案]　B

3．函数y＝log₂x+log_x(2x)的值域为(　)

A．(－∞，－1]　 　　B．[3，+∞)

C．[－1,3]　 　　　　　D．(－∞，－1]∪[3，+∞)

[解析]　y＝log₂x+log_x2+1，

∵log₂x+log_x2≥2或log₂x+log_x2≤－2，

从而y≥3或y≤－1.

[答案]　D