
3.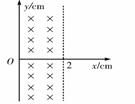 (05年江西)如图所示,宽d = 2cm的有界匀强磁场,纵向范围足够大,磁感应强度的方向垂直纸面向内.现有一群带正电的粒子从O点以相同的速率沿纸面不同方向进入磁场,若粒子在磁场中做匀速圆周运动的轨道半径均为r = 5cm,则 ( AD ) ( )
(05年江西)如图所示,宽d = 2cm的有界匀强磁场,纵向范围足够大,磁感应强度的方向垂直纸面向内.现有一群带正电的粒子从O点以相同的速率沿纸面不同方向进入磁场,若粒子在磁场中做匀速圆周运动的轨道半径均为r = 5cm,则 ( AD ) ( )
A.右边界:-4cm<y≤4cm的范围内有粒子射出
B.右边界:y>4cm和y<-4cm的范围内有粒子射出
C.左边界:y>8cm的范围内有粒子射出
D.左边界:0<y≤8cm的范围内有粒子射出
2.如图所示,在一个水平胶木圆盘上有一个带负电荷的金属块P随圆盘一起绕过Ο点的竖直轴匀速转动,圆盘转动的最大角速度为ω.若在竖直方向加一向下的匀强磁场,仍然保持P随圆盘一起转动,圆盘依图示方向匀速转动的最大角速度为ω′.则下面判断正确的是( BD )
 A.金属块受到的磁场力方向指向圆心O
A.金属块受到的磁场力方向指向圆心O
B.金属块受到的磁场力方向背离圆心O
C.ω<ω′
D.ω>ω′
1. K-介子衰变方程为:K-→?π-?+π0,其中K-介子和π-介子带负的基元电荷,π0介子不带电.如图所示,一个K-介子沿垂直于磁场的方向射入匀强磁场中,其轨迹为圆弧AP,衰变后产生的π-介子的轨迹为圆弧PB,两轨迹在P点相切,它们的半径R1与R2之比为2∶1,π0介子的轨迹未画出.由此可知π-的动量大小与π0的动量大小之比为 ( A )
K-介子衰变方程为:K-→?π-?+π0,其中K-介子和π-介子带负的基元电荷,π0介子不带电.如图所示,一个K-介子沿垂直于磁场的方向射入匀强磁场中,其轨迹为圆弧AP,衰变后产生的π-介子的轨迹为圆弧PB,两轨迹在P点相切,它们的半径R1与R2之比为2∶1,π0介子的轨迹未画出.由此可知π-的动量大小与π0的动量大小之比为 ( A )
A.1∶1 B.1∶2 C.1∶3 D.1∶6
2.带电粒子在洛伦兹力作用下的运动
(1)若带电粒子沿磁场方向射入磁场,即粒子速度方向与磁场方向平行,θ=0°或180°时,带电粒子不受洛伦兹力作用,即F=0,则粒子在磁场中以速度υ做匀速直线运动.
(2)若带电粒子的速度方向与匀强磁场方向垂直,即θ=90°时,带电粒子所受洛伦兹力F=Bqυ,方向总与速度υ垂直.由洛伦兹力提供向心力,使带电粒子在匀强磁场中做匀速圆周运动.求解此类问题的关键是分析并画出空间几何图形--轨迹图.
规律方法
[例1]一个长螺线管中通有电流,把一个带电粒子沿中轴线射入(若不计重力影响),粒子将在管中 ( D )
A.做圆周运动 B.沿轴线来回运动
C.做匀加速直线运动 D.做匀速直线运动
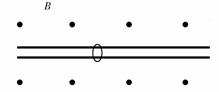 训练题如图所示,一个带负电的滑环套在水平且足够长的粗糙的绝缘杆上,整个装置处于方向如图所示的匀强磁场B中.现给滑环施以一个水平向右的瞬时冲量,使其由静止开始运动,则滑环在杆上的运动情况可能是 ( ABC )
训练题如图所示,一个带负电的滑环套在水平且足够长的粗糙的绝缘杆上,整个装置处于方向如图所示的匀强磁场B中.现给滑环施以一个水平向右的瞬时冲量,使其由静止开始运动,则滑环在杆上的运动情况可能是 ( ABC )
A.始终作匀速运动
B.开始作减速运动,最后静止于杆上
C.先作加速运动,最后作匀速运动
D.先作减速运动,最后作匀速运动
[例2]如图所示,一束电子(电量为e)以速度υ垂直射入磁感应强度为B,宽度为d的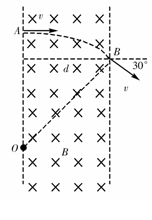 匀强磁场中,穿透磁场时速度方向与电子原来入射方向的夹角是30°,则电子的质量是,穿透磁场的时间是 .
匀强磁场中,穿透磁场时速度方向与电子原来入射方向的夹角是30°,则电子的质量是,穿透磁场的时间是 .
[解析]电子在磁场中运动,只受洛仑兹力作用,故其轨迹是圆弧的一部分,又因为B⊥υ,故圆心在电子穿入和穿出磁场时受到洛仑兹力指向交点上,由几何知识知,AB间圆心角θ=30°,OB为半径.
∴r = = 2d,又由r = 得m =
又∵AB圆心角是30°∴穿透时间t = ,故t = .
训练题如图(甲)所示,在x≥0区域内有如图(乙)所示的大小不变、方向随时间周期性变化的磁场,设磁场方向垂直于纸面向外时为正方向.现有一质量为m、带电量为+q的离子,在t=0时刻从坐标原点O以速度υ沿与x轴正方向成75°角射入,离子运动一段时间而到达P点,P点坐标为(a,a),此时离子的速度方向与?OP?延长线的夹角为30°,离子在此过程中只受磁场力作用.
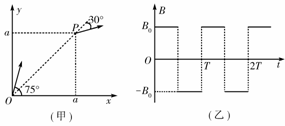 (1)若B0 = B1为已知量,试求离子在磁场中运动时的轨道半径R及周期的表达式.
(1)若B0 = B1为已知量,试求离子在磁场中运动时的轨道半径R及周期的表达式.
(2)若B0为未知量,那么所加最大磁场的变化周期T、磁感应强度B0的大小各应满足什么条件,才能使离子完成上述运动?(写出T、B0各应满足条件的表达式)
答案:(1)T=2πm/qB1,R=mv/qB1
(2)B0=mv/(2)1/2aq,T≥1(2)1/2πa/3v
[例3]如图所示,在y>0的区域内存在匀强磁场,磁场垂直于图中的Oxy平面,方向指向纸外,原点O处有一离子源,沿各个方向射出速率相等的同价负离子,对于进入磁场区域的离子,它们在磁场中做圆弧运动的圆心所在的轨迹,可用图2-7-8给出的四个半圆中的一个来表示,其中正确的是 ( C )

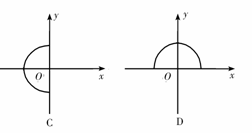
训练题(05年高考科研)一质点在一平面内运动,其轨迹如图所示,它从A点出发,以恒定速率v0经时间t到B点,图中x轴上方的轨迹都是半径为R的半圆,下方的都是半径为r的半圆
(1)求此质点由A到B沿x轴运动的平均速度;
(2)如果此质点带正电,且以上运动是在一恒定(不随时间而变)的磁场中发生的,试尽
 可能详细地论述此磁场的分布情况,不考虑重力的影响。
可能详细地论述此磁场的分布情况,不考虑重力的影响。
答案:(1)v= =
=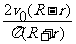 (2)论述略,
(2)论述略,
能力训练
1.洛伦兹力:
(1)产生洛伦兹力的条件:①电荷对磁场有相对运动.磁场对与其相对静止的电荷不会产生洛伦兹力作用.②电荷的运动速度方向与磁场方向不平行.
(2)洛伦兹力大小:当电荷运动方向与磁场方向平行时,洛伦兹力为零;当电荷运动方向与磁场方向垂直时,洛伦兹力最大,等于qυB;
(3)洛伦兹力的方向:洛伦兹力方向用左手定则判断
(4)洛伦兹力不做功.
22.解析(Ⅰ)由抛物线方程得其准线方程: ,根据抛物线定义
,根据抛物线定义
点 到焦点的距离等于它到准线的距离,即
到焦点的距离等于它到准线的距离,即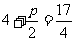 ,解得
,解得
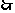 抛物线方程为:
抛物线方程为: ,将
,将 代入抛物线方程,解得
代入抛物线方程,解得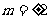
(Ⅱ)由题意知,过点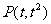 的直线
的直线 斜率存在且不为0,设其为
斜率存在且不为0,设其为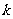 。
。
则 ,当
,当 则
则 。
。
联立方程 ,整理得:
,整理得: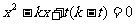
即: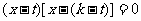 ,解得
,解得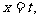 或
或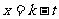
 ,而
,而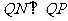 ,
,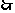 直线
直线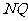 斜率为
斜率为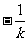
 ,联立方程
,联立方程
整理得: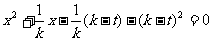 ,即:
,即:
 ,解得:
,解得: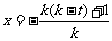 ,或
,或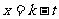
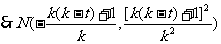 ,
,
而抛物线在点N处切线斜率: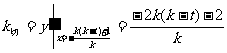
 MN是抛物线的切线,
MN是抛物线的切线,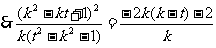 , 整理得
, 整理得
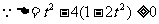 ,解得
,解得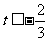 (舍去),或
(舍去),或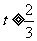 ,
,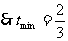
20、解析:(Ⅰ)当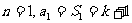 ,
,
 (
( )
)
经验,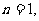 (
( )式成立,
)式成立,
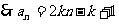
(Ⅱ)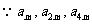 成等比数列,
成等比数列,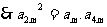 ,
,
即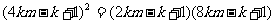 ,整理得:
,整理得: ,
,
对任意的 成立,
成立,

|
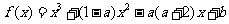
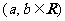 .
.
(I)若函数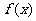 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,求
,求 的值;
的值;
(II)若函数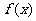 在区间
在区间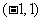 上不单调,求
上不单调,求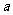 的取值范围.
的取值范围.
解析:(Ⅰ)由题意得
又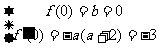 ,解得
,解得 ,
,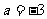 或
或
(Ⅱ)函数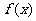 在区间
在区间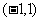 不单调,等价于
不单调,等价于
导函数 在
在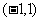 既能取到大于0的实数,又能取到小于0的实数
既能取到大于0的实数,又能取到小于0的实数
即函数 在
在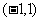 上存在零点,根据零点存在定理,有
上存在零点,根据零点存在定理,有
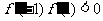 , 即:
, 即: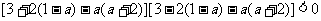
整理得: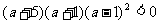 ,解得
,解得

|
 :
: 上一点
上一点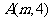 到其焦点的距离为
到其焦点的距离为 .
.
(I)求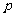 与
与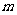 的值;
的值;
(II)设抛物线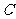 上一点
上一点 的横坐标为
的横坐标为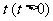 ,过
,过 的直线交
的直线交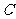 于另一点
于另一点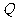 ,交
,交 轴于
轴于
点 ,过点
,过点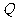 作
作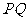 的垂线交
的垂线交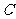 于另一点
于另一点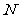 .若
.若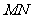 是
是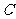 的切线,求
的切线,求 的最小值.
的最小值.
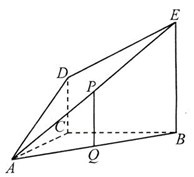
19.(Ⅰ)证明:连接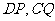 , 在
, 在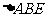 中,
中,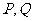 分别是
分别是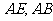 的中点,所以
的中点,所以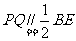 , 又
, 又 ,所以
,所以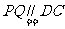 ,又
,又 平面ACD ,DC
平面ACD ,DC 平面ACD, 所以
平面ACD, 所以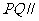 平面ACD
平面ACD
(Ⅱ)在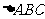 中,
中,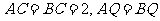 ,所以
,所以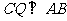
而DC 平面ABC,
平面ABC,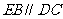 ,所以
,所以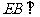 平面ABC
平面ABC
而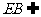 平面ABE, 所以平面ABE
平面ABE, 所以平面ABE 平面ABC, 所以
平面ABC, 所以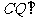 平面ABE
平面ABE
由(Ⅰ)知四边形DCQP是平行四边形,所以
所以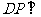 平面ABE, 所以直线AD在平面ABE内的射影是AP,
平面ABE, 所以直线AD在平面ABE内的射影是AP,
所以直线AD与平面ABE所成角是
在 中,
中, ,
,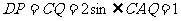
所以
|
 为数列
为数列 的前
的前 项和,
项和, ,
,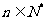 ,其中
,其中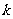 是常数.
是常数.
(I) 求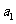 及
及 ;
;
(II)若对于任意的 ,
,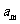 ,
, ,
,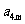 成等比数列,求
成等比数列,求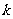 的值.
的值.
|
 中,角
中,角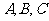 所对的边分别为
所对的边分别为 ,且满足
,且满足 ,
,
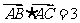 .
(I)求
.
(I)求 的面积;
(II)若
的面积;
(II)若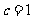 ,求
,求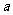 的值.
的值.
18.解析:(Ⅰ)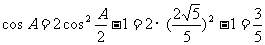
又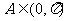 ,
,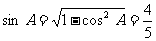 ,而
,而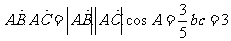 ,所以
,所以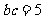 ,所以
,所以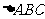 的面积为:
的面积为: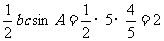
(Ⅱ)由(Ⅰ)知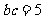 ,而
,而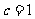 ,所以
,所以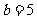
所以
|
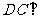 平面
平面 ,
,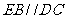 ,
,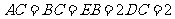 ,
, ,
,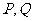 分别为
分别为 的中点.(I)证明:
的中点.(I)证明: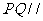 平面
平面 ;(II)求
;(II)求 与平面
与平面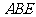 所成角的正弦值.
所成角的正弦值.17.  [命题意图]此题是一个排列组合问题,既考查了分析问题,解决问题的能力,更侧重于考查学生便举问题解决实际困难的能力和水平
[命题意图]此题是一个排列组合问题,既考查了分析问题,解决问题的能力,更侧重于考查学生便举问题解决实际困难的能力和水平
[解析]对于大于14的点数的情况通过列举可得有5种情况,即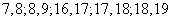 ,而基本事件有20种,因此
,而基本事件有20种,因此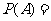

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com