
1. 人称代词不仅仅指人,也可以指事或物。
(二)激励启发、诊断引导
2、一套练习题,有几十个题目,有的难,有的易,教师可以抓一个难的题目给大家讲解,作示范,然后,把这套练习题进行分组。比如,选择题,可以每10个一组(当然不分组也可以),让学生提问。教师指导学生提问:“你认为这10个题目中最难的是哪一个?难在何处?”教师随堂解答,有点答记者问的意思。
[例1]三国鼎立时下列哪一地区经济发展水平最高
A.黄河流域 B.江东地区 C.南中地区 D.荆州地区
教材中没有各地经济发展的具体数据,是不是“超纲”了呢?这一分裂时期,三国的军事实力大体相当,但黄河流域经济基础较好,且曹魏政权重视恢复和发展经济,为西晋统一全国奠定了坚实的物质基础,最后由三国分裂走向西晋的统一,完全可推导出A正确。
这道题可以改编成问答题:三国鼎立局面形成的基本原因是什么?这种局面形成是否具有进步性?说明理由。题中的“进步性”实际上就是指“统一因素”。
现在,很多专家、学者都强调,在教学中,要激发学生学习的兴趣,要培养学生学习的习惯、学习的能力,最重要的是要多设疑,让学生提问。而怎样设疑、怎样提问,却是大家关注的问题,没有一条明确的路径可循。高三学生已经掌握了相当的知识,怎样应用?怎样提问?以前,我们教学生做题,总习惯于“做题--对答案--个别纠正”。从教育学角度看,它注重的是教育者的活动,而没有注意到或很少注意到受教育者的活动。其次,人们对教育对象--学生解历史题,长期的意识是“背书”,近几年,高考能力题含量的增加,又把学生送进题海中去了。这只关心了学生知不知的问题,没有关心学生信不信、行不行的问题。到底有没有一种既能提高学生解历史题的能力,又能避免学生在题海中泡得时间太长而疲软的状态,促进学生“知”“情”“行”和谐统一,乐于接受和实践的有效方法?就此,我想从解析习题来谈点看法,抛砖引玉吧。
习题,是教师、命题人就某一单元或全体内容设计的问题,用来检验学生所学知识的一种形式,它是课堂教学的一个有机组成部分和延伸,是学习者对学习任务的重复接触或重复反应,但不是活动的简单重复,而是一种有目的、有步骤、有指导的活动,是一个自觉的、具有创造性成分的过程。做习题,是学生巩固所学知识的一种重要途径;做习题,是学生把所学的知识应用到“实践”中来的一个重要表现;做习题,是教师检测学生学到了多少知识、会理解与应用多少知识的一个重要手段。
会解题目,不能只满足于做出答案;会解题目,应该“解析”题目的题干和题枝,从分析题目中,理解、应用所学的知识及原理,分析、体会命题人的良苦用心,获取知识、培养能力(学习能力、分析能力、迁移能力、应用能力)、接受教育(人生观、道德情操、爱国主义、国防安全观念等等)。
22.如图,已知平面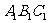 平行于三棱锥
平行于三棱锥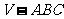 的底面,等边三角形
的底面,等边三角形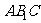 所在平面与面
所在平面与面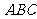 垂直,且
垂直,且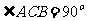 ,设
,设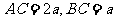 。
。
(1证明: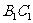 为异面直线
为异面直线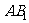 与
与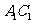 的公垂线;
的公垂线;
(2求点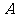 与平面
与平面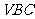 的距离;
的距离;
(3求二面角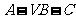 的大小。
的大小。
2007-2008学年度南昌市高三第一轮复习训练题
21.
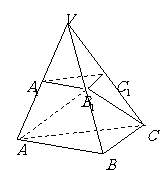
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形,
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形,
∠ABC=∠BAD=90°,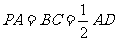 .
.
(1)求证:平面PAC⊥平面PCD;
(2)在棱PD上是否存在一点E,使CE//平面PAB?
若存在,请确定E点的位置;若不存在,请说明理由
20.如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,
⑴求证:A1C⊥平面BDE;
⑵求A1B与平面BDE所成角的正弦值。
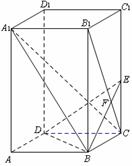
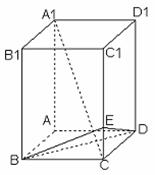
19. 如图6所示,在长方体ABCD-A1B1C1D1中,AB = BC = 1,
BB1 = 2,正是棱CC1上的点,且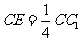
(1)求三棱锥C-BED的体积;
(2)求证:A1C⊥平面BDE.
.
18.如图,已知DA⊥平面ABE,四边形ABCD是边长为2的正方形,
在△ABE中,AE=1,BE=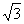
(1)证明:平面ADE⊥平面BCE;
(2)求二面角B-AC-E的余弦值。
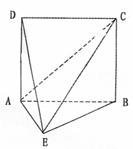
17.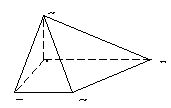 如图,在四棱锥
如图,在四棱锥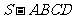 中,
中, 平面
平面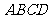 ,
,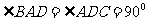 ,
,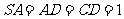 ,
,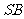 与平面
与平面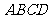 所成角的大小是
所成角的大小是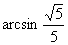 .
.
 (1)求四棱锥
(1)求四棱锥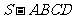 的体积;
的体积;
(2)求异面直线 与
与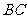 所成角的大小.
所成角的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com