5、课堂小结：
[问7]①今天这节课主要学习了什么内容？
②在问题的解决过程中，我们运用了那些数学思想？
[答]①回顾从具体到抽象的研究方法；
②掌握运用辗转相除法求两个正整数的最大公约数；
③体会迭代算法思想。
[设计意图]使学生对本节课所学知识的结构有一个清晰的认识，对本节课所用的迭代算法数学思想方法有一个明确的了解。
4、应用辗转相除法算法
[练2]右面一段伪代码的目的是：( )
A.求x,y的最小公倍数 B.求x,y的最大公约数
C.求x被y整除的商 D. 求y被x整除的商
[生答] B
[设计意图]会“ 识”直到型循环语句描述的应用辗转相除法求最大公约数。
|
A.1 B.429
C.190 D.6
[生答] A
[设计意图]会“识”当型循环语句描述辗转相除法
并且会“算”最大公约数。
[练4]设计计算两个正整数
的
最小公倍数的算法。
[设计意图]会“用”辗转相除法的算法语句。
[师提示]最小公倍数＝
[生演板]
|
|
|
[问6]：还有其他算法吗？
[生答]运用案例1穷举算法方法
[设计意图]①巩固练习辗转相除法算法；②重温上节课孙子问题的穷举算法思想。
3、设计辗转相除法算法
[问4]写出两个正整数的最大公约数的一个算法。
[师初步分析]运用辗转相除法，产生一列数：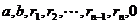
。这列数从第三项开始，每项都是前两项相除所得的余数，余数为0的前一项
，既是
和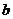
的最大公约数。
递推关系：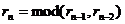
(其中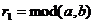
，
)
[问5]可选用什么结构书写此算法？
[生答]循环结构。
[生分组讨论]共分为两个小组，分别用直到型和当型循环结构写算法、画流程图和写伪代码，并派代表演板流程图和伪代码。
|
 |
|||
|
|
|
||||
[师点评结果]通过演板的流程图和伪代码的对比，梳理算法，
|
[设计意图]
①多角度分析问题，加强综合运用知识能力；
②通过小组合作探索，激发学生兴趣，巩固新知；
③渗透从具体到抽象的数学思想方法，体会迭代
的算法思想。
2、理解辗转相除法原理
[问2]22与6的最大公约数？
[设计意图]把辗转相除法和情景设置联系起来，承上启下，顺利过渡。
[问3]204与85的最大公约数？
[师板书] 204＝85×2+34
85 ＝ 34×2+17
34 ＝ 17×2+0 ＝> 204与85最大公约数为17。
[师引导]总结辗转相除法具体步骤。
[师讲解]辗转相除法原理：(204，85)＝(85，34)＝(34，17)。
[练1]求678与35的最大公约数？
[设计意图]具体动手操作，巩固新知。
1、情景设置――感知辗转相除法
(发给每位学生一张长为22cm，宽为6cm的纸条)
[问1]这张长方形的纸，先拿短边往长边上折，得到一个正方形，从长方形上裁掉这个正方形后继续将短边往长边上折，一直到最后剩下来的是正方形为止，最后得到的边长是几的正方形？
[师生互动解答]22＝6×3+4；
6 ＝ 4×1+2；
4 ＝ 2×2+0 ＝> 最后正方形的边长为2cm。
[设计意图]通过动手操作，直观感受辗转相除法的具体做法。
2、学法：以观察、讨论、思考、分析、动手操作、自主探索、合作学习多种形式相结合，引导学生多角度、多层面认识事物，突破教学难点。
1、教法：以问题为载体，有引导的对话，让学生经历知识的形成过程和发展过程，从而突出教学重点，并采用多媒体教学，增加课堂容量，有利于学生活动的充分展开。
3、教学重点与难点：
(1)教学重点：
①理解辗转相除法原理；
②能用自然语言、流程图和伪代码表达辗转相除法。
(2)教学难点：
①理解和区分两种循环结构表达辗转相除法；
②能应用迭代算法思想。
2、教学目标：
(1)知识目标：
①理解辗转相除法原理；
②能用自然语言、流程图和伪代码表达辗转相除法；
③能应用迭代算法思想。
(2)能力目标：
①培养学生把具体问题抽象转化为算法语言的能力；
②培养学生自主探索和合作学习的能力。
(3)情感目标：
①使学生进一步了解从具体到抽象，抽象到具体的辨证思想方法，对学生进行辨证唯物主义教育；
②创设和谐融洽的教学氛围和阶梯形问题，使学生在活动中获得成功感，从而培养学生热爱数学、积极学习数学、应用数学的热情。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，则输出最大公约数b；若
，则转S3。
的余数；
；
x