
13.(05重庆卷)设函数f(x)2x33(a1)x26ax8,其中aÎR。
(1) 若f(x)在x3处取得极值,求常数a的值;
(2) 若f(x)在(¥,0)上为增函数,求a的取值范围。
12. (山东卷)已知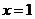 是函数
是函数 的一个极值点,其中
的一个极值点,其中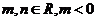 .
.
(I)求 与
与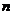 的关系式;
的关系式;
(II)求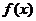 的单调区间;
的单调区间;
(III)当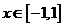 时,函数
时,函数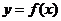 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3 ,求
,求 的取值范围.
的取值范围.
11.(湖南卷)已知函数f(x)=lnx,g(x)=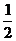 ax2+bx,a≠0.
ax2+bx,a≠0.
(Ⅰ)若b=2,且h(x)=f(x)-g(x)存在单调递减区间,求a的取值范围;
(Ⅱ)设函数f(x)的图象C1与函数g(x)图象C2交于点P、Q,过线段PQ的中点作x轴的垂线分别交C1,C2于点M、N,证明C1在点M处的切线与C2在点N处的切线不平行.
10. (05北京卷)过原点作曲线y=ex的切线,则切点的坐标为 ;切线的斜率为 .
9.(05江苏卷)曲线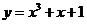 在点(1,3)处的切线方程是
在点(1,3)处的切线方程是
8. (05重庆卷)曲线yx3在点(1,1)处的切线与x轴、直线x2所围成的三角形的面积为__.
7.已知函数f(x)满足:f(3)=2,
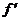 (3)=-2, 则极限
(3)=-2, 则极限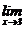
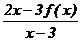 的值为___________
的值为___________
6.已知在函数y=x3+ax2-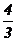 a中,
a中,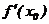 =0 且f(xo)=0, 则a的值为____________
=0 且f(xo)=0, 则a的值为____________
5.(2003年普通高等学校招生全国统一考试(上海卷理工农医类16))
f(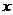 )是定义在区间[-c,c]上的奇函数,其图象如图所示:令g(
)是定义在区间[-c,c]上的奇函数,其图象如图所示:令g(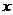 )=af(
)=af(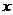 )+b,则下
)+b,则下
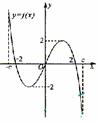 列关于函数g(
列关于函数g( )的叙述正确的是(
)
)的叙述正确的是(
)
A.若a<0,则函数g( )的图象关于原点对称.
)的图象关于原点对称.
B.若a=-1,-2<b<0,则方程g( )=0有大于2的实根.
)=0有大于2的实根.
C.若a≠0,b=2,则方程g(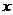 )=0有两个实根.
)=0有两个实根.
D.若a≥1,b<2,则方程g(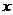 )=0有三个实根.
)=0有三个实根.
4.设f(x)在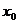 处可导,下列式子中与
处可导,下列式子中与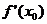 相等的是
(
)
相等的是
(
)
(1)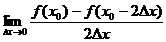 ; (2)
; (2)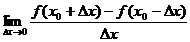 ;
;
(3)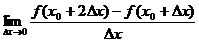 (4)
(4)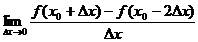 。
。
A.(1)(2) B.(1)(3) C.(2)(3) D.(1)(2)(3)(4)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com